зҺҜзҗғи§Ӯз„ҰзӮ№пјҡеҗҲж•°зҡ„е®ҡд№үжҳҜд»Җд№ҲдҪ зҹҘйҒ“еҗ— е®ғжң¬иҙЁдёҠжҳҜеҗҰе°ұжҳҜдёҖдёӘиҙЁж•°
йҡҸзқҖзӨҫдјҡи¶ҠжқҘи¶ҠеҸ‘иҫҫпјҢеӨ§е®¶йғҪйҖүжӢ©еңЁзҪ‘з»ңдёҠжұІеҸ–зӣёе…ізҹҘиҜҶеҶ…е®№пјҢжҜ”еҰӮеҗҲж•°зҡ„е®ҡд№үпјҲеҗҲж•°зҡ„е®ҡд№үжҳҜд»Җд№Ҳпјү пјҢдёәдәҶжӣҙеҘҪзҡ„и§Јзӯ”еӨ§е®¶зҡ„й—®йўҳпјҢе°Ҹзј–д№ҹжҳҜзҝ»йҳ…ж•ҙзҗҶдәҶзӣёеә”еҶ…е®№пјҢдёӢйқўе°ұдёҖиө·жқҘзңӢдёҖдёӢеҗ§пјҒ
ж•ҙж•°еҢ…жӢ¬жӯЈж•ҙж•°е’Ңиҙҹж•ҙж•°пјӣиҮӘ然数дёәaxeж•ҙж•°(еҗ«0)пјӣдёҚжҳҜ2зҡ„еҖҚж•°зҡ„ж•°жҳҜеҘҮж•°пјӣжҳҜ2зҡ„еҖҚж•°зҡ„ж•°жҳҜеҒ¶ж•°пјӣеҰӮжһңдёҖдёӘж•°еҸӘжңү1е’Ңе®ғиҮӘе·ұзҡ„дёӨдёӘеӣ еӯҗпјҢиҝҷж ·зҡ„ж•°жҳҜиҙЁж•°пјӣеҰӮжһңдёҖдёӘж•°йҷӨдәҶ1е’Ңе®ғжң¬иә«иҝҳжңүе…¶д»–еӣ еӯҗпјҢиҝҷж ·зҡ„ж•°еҸ«еҒҡеҗҲж•°гҖӮеҰӮжһң3е‘ўпјҹ4=12пјҢйӮЈд№Ҳ3е’Ң4жҳҜ12зҡ„еӣ ж•°пјҢ12жҳҜ3е’Ң4зҡ„еҖҚж•°гҖӮеӣ еӯҗе’ҢеҖҚж•°жҳҜзӣёдә’дҫқеӯҳзҡ„пјҢдёҚиғҪеҚ•зӢ¬еӯҳеңЁгҖӮ
 гҖҗиө„ж–ҷеӣҫгҖ‘
гҖҗиө„ж–ҷеӣҫгҖ‘
еҗҲж•°жҳҜжҢҮеңЁеӨ§дәҺ1зҡ„ж•ҙж•°дёӯпјҢйҷӨдәҶ1е’Ңе®ғжң¬иә«д№ӢеӨ–пјҢиҝҳиғҪиў«е…¶д»–ж•°(йҷӨдәҶ0)ж•ҙйҷӨзҡ„ж•°гҖӮзӣёжҜ”иҫғиҖҢиЁҖпјҢе®ғжҳҜдёҖдёӘиҙЁж•°пјҢ1ж—ўдёҚжҳҜиҙЁж•°пјҢд№ҹдёҚжҳҜеҗҲж•°гҖӮзҡ„жңҖе°ҸеҲҶи§Јж•°жҳҜ4гҖӮиҝҷдёӘе®ҢзҫҺж•°еӯ—е’ҢзӣёдәІж•°еӯ—е°ұжҳҜд»Ҙе®ғдёәеҹәзЎҖзҡ„гҖӮ
жҜҸдёҖдёӘеҗҲж•°йғҪеҸҜд»ҘеңЁиҝҮзЁӢдёӯдёўеӨұеӨҡе°‘дёӘзҙ ж•°пјҢдёҖдёӘеҗҲж•°д№ҹеҸҜд»ҘеңЁиҝҮзЁӢдёӯдёўеӨұеӨҡе°‘дёӘзҙ ж•°гҖӮ
ж №жҚ®ж•°еӯҰпјҢиҙЁж•°жҳҜеҸӘиғҪиў«иҮӘиә«ж•ҙйҷӨзҡ„йқһйӣ¶иҮӘ然数пјҢйҷӨдәҶиғҪиЎҘ1зҡ„ж•ҙж•°гҖӮжҜ”еҰӮ5пјҢ11зӯүзӯүйғҪжҳҜиҙЁж•°гҖӮеҗҲж•°жҳҜиғҪиў«йҷӨ1е’ҢиҮӘиә«д»ҘеӨ–зҡ„е…¶д»–ж•°ж•ҙйҷӨзҡ„йқһйӣ¶иҮӘ然数пјҢеҰӮ6е’Ң9гҖӮеҘҮж•°жҳҜдёҚиғҪиў«2ж•ҙйҷӨзҡ„йқһйӣ¶иҮӘ然数гҖӮжҜ”еҰӮ1пјҢ3пјҢ5зӯүзӯүйғҪжҳҜеҘҮж•°гҖӮеҒ¶ж•°жҳҜиғҪиў«2ж•ҙйҷӨзҡ„иҮӘ然数гҖӮдҫӢеҰӮпјҢ4гҖҒ6гҖҒ8зӯүгҖӮйғҪжҳҜеҒ¶ж•°гҖӮ
зҙ ж•°жҳҜйҷӨдәҶиҮӘиә«е’Ң1д№ӢеӨ–жІЎжңүе…¶д»–еӣ еӯҗзҡ„ж•°пјҢеҚійҷӨдәҶиҮӘиә«е’Ң1д№ӢеӨ–иҝҳжңүе…¶д»–еӣ еӯҗзҡ„ж•°гҖӮиҝҷйҮҢж¶үеҸҠеҲ°еӨҡе°‘и§ӮзӮ№:(1)еӣ зҙ гҖӮз®ҖеҚ•жқҘиҜҙпјҢеҰӮжһңдёҖдёӘж•°AжҳҜеҸҰдёҖдёӘж•°Bзҡ„еҖҚж•°(еҚіAиғҪиў«Bж•ҙйҷӨ)пјҢйӮЈд№ҲBе°ұжҳҜAзҡ„еӣ еӯҗ(2)дҪңдёәдёҖдёӘвҖңзҙ ж•°вҖқе’ҢдёҖдёӘвҖңеҗҲж•°вҖқпјҢе®ғеұһдәҺе°ҸеӯҰж•ҷеӯҰйўҶеҹҹпјҢе°ұеғҸжҲ‘们иҝҷйҮҢиҜҙзҡ„гҖӮд№ҹе°ұжҳҜ1пјҢ2пјҢ3пјҢ4пјҢ5...жҜ”еҰӮпјҢз”ұдәҺ5дёҚиғҪиў«1е’Ң5д№ӢеӨ–зҡ„е…¶дҪҷж•°ж•ҙйҷӨпјҢжүҖд»Ҙ5жҳҜиҙЁж•°пјҢ6еҸҜд»Ҙиў«2е’Ң3ж•ҙйҷӨпјҢжүҖд»Ҙ6жҳҜеҗҲж•°гҖӮ
жү©еұ•дҝЎжҒҜ:
д№ӢдёҖпјҢиҙЁж•°зҡ„ж°”иҙЁ
1.зҙ ж•°pеҸӘжңүдёӨдёӘзәҰж•°:1е’ҢpгҖӮ
2.еҲқзӯүж•°еӯҰеҹәжң¬е®ҡзҗҶ:д»»дҪ•еӨ§дәҺ1зҡ„иҮӘ然数пјҢиҰҒд№Ҳжң¬иә«е°ұжҳҜзҙ ж•°пјҢиҰҒд№ҲеҸҜд»Ҙи§ЈжһҗдёәеӨҡдёӘзҙ ж•°зҡ„д№ҳз§ҜпјҢиҝҷдёӘеҲҶжһҗжҳҜе”ҜдёҖзҡ„гҖӮ
3.иҙЁж•°зҡ„ж•°йҮҸжҳҜж— йҷҗзҡ„гҖӮ
4.зҙ ж•°ПҖ(n)зҡ„ж•°е…¬ејҸжҳҜдёҖдёӘдёҚеҮҸеҮҪж•°гҖӮ
5.еҰӮжһңnжҳҜжӯЈж•ҙж•°пјҢn2е’Ң(n+1)2д№Ӣй—ҙиҮіе°‘жңүдёҖдёӘзҙ ж•°гҖӮ
дәҢгҖҒеҘҮејӮж°”иҙЁ
1.жүҖжңүеӨ§дәҺ2зҡ„еҒ¶ж•°йғҪжҳҜеҗҲж•°гҖӮ
2.еңЁжүҖжңүеӨ§дәҺ5зҡ„еҘҮж•°дёӯпјҢеёҰ5зҡ„ж•°жҳҜеҗҲж•°гҖӮ
3.йҷӨдәҶ0пјҢжүҖжңүеёҰ0зҡ„иҮӘ然数йғҪжҳҜеҗҲж•°гҖӮ
4.жүҖжңүеҚ•дҪҚдёә4гҖҒ6е’Ң8зҡ„иҮӘ然数йғҪжҳҜеҗҲж•°гҖӮ
5.жңҖе°ҸеҒ¶ж•°жҳҜ4пјҢжңҖе°ҸеҘҮж•°жҳҜ9гҖӮ
6.жҜҸдёҖдёӘеҗҲж•°йғҪеҸҜд»ҘеҶҷжҲҗиҙЁж•°д№ҳз§Ҝзҡ„е”ҜдёҖжғ…еҶөпјҢд№ҹе°ұжҳҜеҲҶжһҗиҙЁеӣ ж•°гҖӮ
еҘҮж•°пјҢиғҪиў«2еӣӣиҲҚдә”е…Ҙзҡ„еҸ«еҘҮж•°пјҢдёҚиғҪеӣӣиҲҚдә”е…Ҙзҡ„еҸ«еҒ¶ж•°гҖӮ
иҙЁж•°пјҢеҗҲж•°:иҙЁж•°жҳҜжҢҮжүҖжңүеӨ§дәҺ1зҡ„ж•ҙж•°пјҢйҷӨдәҶ1е’Ңе®ғжң¬иә«пјҢжІЎжңүе…¶д»–йҷӨж•°гҖӮиҝҷдёӘж•ҙж•°еҸ«еҒҡиҙЁж•°жҲ–зҙ ж•°гҖӮд№ҹеҸҜд»ҘиҜҙпјҢдёҖдёӘзҙ ж•°еҸӘжңү1е’Ңе®ғиҮӘе·ұзҡ„дёӨдёӘзәҰж•°пјӣеҗҲж•°пјҢд№ҹз§°дёәеҗҲж•°пјҢжҳҜж»Ўи¶ід»ҘдёӢ(зӯүд»·)еүҚжҸҗд№ӢдёҖзҡ„жӯЈж•ҙж•°:1гҖӮе®ғжҳҜдёӨдёӘеӨ§дәҺ1зҡ„ж•ҙж•°зҡ„д№ҳз§Ҝпјӣ2.жңүдёҖдёӘеӨ§дәҺ1дҪҶе°ҸдәҺиҮӘиә«зҡ„еӣ еӯҗпјӣ3.иҮіе°‘жңүдёүдёӘиҰҒзҙ (еӣ зҙ )пјӣ4.ж—ўдёҚжҳҜ1пјҢд№ҹдёҚжҳҜиҙЁж•°(зҙ ж•°)пјӣ5.иҮіе°‘жңүдёҖдёӘиҙЁеӣ ж•°зҡ„йқһиҙЁж•°гҖӮ
е…¬еӣ ж•°пјҢжңҖе…¬еӣ ж•°:иғҪиў«еӨҡе°‘дёӘж•°ж•ҙйҷӨзҡ„ж•°з§°дёәе…¬еӣ ж•°пјӣе…¶дёӯжӣҙеӨ§зҡ„жҳҜжңҖеёёи§Ғзҡ„еӣ зҙ гҖӮ
е…¬еҖҚж•°пјҢжңҖе°Ҹе…¬еҖҚж•°:еҰӮжһңдёҖз»„ж•°жҳҜдёҖдёӘж•°зҡ„е…¬еҖҚж•°пјҢйӮЈд№ҲиҝҷдёӘж•°е°ұжҳҜиҝҷз»„ж•°зҡ„е…¬еҖҚж•°пјӣжңҖе°Ҹе…¬еҖҚж•°е°ұжҳҜжңҖе°Ҹе…¬еҖҚж•°гҖӮ
иҙЁеӣ ж•°пјҢеҲҶжһҗиҙЁеӣ ж•°:жҜҸдёӘеҗҲж•°дёӯеҸҜд»Ҙзӣёд№ҳеӨҡе°‘дёӘиҙЁж•°зҡ„жғ…еҶөпјҢз§°дёәиҝҷдёӘеҗҲж•°зҡ„иҙЁеӣ ж•°пјӣжҜҸдёӘеҗҲж•°еҸҜд»ҘеҶҷжҲҗеӨҡе°‘дёӘиҙЁж•°зҡ„д№ҳз§ҜпјҹжҜҸдёҖдёӘзҙ ж•°йғҪжҳҜиҝҷдёӘеҗҲж•°зҡ„дёҖдёӘеӣ еӯҗпјҢз§°дёәиҝҷдёӘеҗҲж•°зҡ„зҙ ж•°еӣ еӯҗзҡ„йҳ¶д№ҳеҲҶжһҗгҖӮеҲҶжһҗиҙЁеӣ ж•°еҸӘйҖӮз”ЁдәҺеҗҲж•°гҖӮ
дә’иҙЁ:дёӨдёӘжңҖе…¬еӣ ж•°дёә1зҡ„иҮӘ然数称дёәдә’иҙЁж•°гҖӮдёӨдёӘд»ҘдёҠзҡ„ж•°жҳҜжңҖеёёи§Ғзҡ„еӣ ж•°пјҢдёӨдёӘеҸӘжңү1зҡ„ж•°жҳҜиҙЁж•°гҖӮ
еҒ¶ж•°:иғҪиў«2ж•ҙйҷӨзҡ„ж•°еҸҜд»Ҙйҡҗеҗ«дёә2aгҖӮ
еӣ еӯҗ:еңЁж•ҙж•°ж ҮеәҰдёӯпјҢaГ·b=c(bвү 0)cжҳҜжІЎжңүдҪҷж•°зҡ„ж•ҙж•°пјҢbжҳҜaзҡ„еӣ еӯҗгҖӮ
иҙЁж•°:еҸӘжңү1е’Ңе®ғжң¬иә«зҡ„дёӨдёӘеӣ еӯҗеҰӮaпјҢaзҡ„еӣ еӯҗжҳҜ1пјҢaгҖӮ
еҗҲж•°:йҷӨдәҶ1е’Ңе®ғжң¬иә«пјҢиҝҳжңүAзӯүе…¶д»–еӣ еӯҗпјҢAзҡ„еӣ еӯҗжҳҜ1пјҢmвҖҰвҖҰa A AгҖӮ
0жҳҜеҒ¶ж•°пјҢжҳҜжүҖжңүж•°зҡ„еҖҚж•°пјҢ1жҳҜжүҖжңүж•°зҡ„еӣ ж•°пјҢ1ж—ўдёҚжҳҜиҙЁж•°пјҢд№ҹдёҚжҳҜеҗҲж•°гҖӮ
иҙЁж•°жҳҜжҢҮеӨ§дәҺ1зҡ„иҮӘ然数дёӯпјҢеҸӘжңү1е’Ңе®ғжң¬иә«дҪңдёәеӣ еӯҗзҡ„ж•°гҖӮеҗҲж•°жҳҜжҢҮйҷӨдәҶ1е’Ңе®ғжң¬иә«д№ӢеӨ–пјҢиҝҳиғҪиў«е…¶д»–ж•°(йҷӨдәҶ0)ж•ҙйҷӨзҡ„ж•°гҖӮ
00д»ҘеҶ…зҡ„иҙЁж•°жҳҜ:2пјҢ3пјҢ5пјҢ7пјҢ11пјҢ13пјҢ17пјҢ19пјҢ23пјҢ29пјҢ31пјҢ37пјҢ41пјҢ43пјҢ47пјҢ53пјҢ59пјҢ61пјҢ67пјҢ71пјҢ73пјҢ79пјҢ83пјҢ89пјҢ.е®ғеӨ§дәҺжҲ–зӯүдәҺ4зҡ„еҒ¶ж•°пјӣ4дҪҚгҖҒ6дҪҚе’Ң8дҪҚиҮӘ然数гҖӮеҸҰеӨ–пјҢйҷӨдәҶ0пјҢжүҖжңүж•°еӯ—дёә0зҡ„иҮӘ然数йғҪжҳҜеҗҲж•°гҖӮ
жү©еұ•дҝЎжҒҜ:
еҫҲеӨҡеҘҪзҡ„з”өеҪұпјҢжҜ”еҰӮгҖҠжқҖйҳөгҖӢгҖҒгҖҠйһӢеӯҗгҖӢгҖҒгҖҠй•ңеӯҗйҮҢзҡ„дёӨеј и„ёгҖӢгҖҒгҖҠжјӮдә®зҡ„еӨҙи„‘гҖӢпјҢйғҪиЎЁзҺ°дәҶдәәж°‘зҫӨдј—еҜ№зҙ ж•°е’Ңжҡ—еҸ·зҡ„зҘһз§ҳж„ҹзҡ„жҖҖеҝөгҖӮеңЁдҝқзҪ—В·д№”В·е”җиҜәзҡ„е°ҸиҜҙгҖҠиҙЁж•°зҡ„еӯӨзӢ¬гҖӢдёӯпјҢиҙЁж•°иў«з”ЁдҪңеӯӨзӢ¬е’ҢеҜӮеҜһзҡ„йҡҗе–»пјҢиў«жҸҸиҝ°дёәж•ҙж•°д№Ӣй—ҙзҡ„вҖңеұҖеӨ–дәәвҖқгҖӮ
д»ҘдёҠеҶ…е®№е°ұжҳҜдёәеҗ„дәәеҲҶдә«зҡ„еҗҲж•°зҡ„з•ҢиҜҙпјҲеҗҲж•°зҡ„з•ҢиҜҙжҳҜд»Җд№Ҳпјүзӣёе№ІеёёиҜҶпјҢж„ҝжңӣеҜ№дҪ жңүжүҖеё®еҝҷ пјҢеҒҮеҰӮиҝҳжғіжҗңеҜ»е…¶дҪҷжҲҗз»©пјҢиҜ·зҸҚи—Ҹжң¬зҪ‘з«ҷжҲ–зӮ№еҮ»жҗңеҜ»жӣҙеӨҡжҲҗз»©гҖӮ\- е…Ёзҗғеҝ«иө„и®ҜдёЁеҲ«е…Ӣе…Ёж–°дёҖд»ЈGL8 ESиұӘеҚҺе•Ҷж—…иҪҰ иҜ•й©ҫдјҡ
- еҫ®дҝЎжҖҺд№ҲжӢүжңӢеҸӢиҝӣеҺ»пјҲеҫ®дҝЎжҖҺд№ҲжӢүжңӢеҸӢиҝӣзҫӨпјү
- иӢ№жһңжҷәиғҪжҲ’жҢҮиҰҒжқҘдәҶпјҹеӨ§йҮҸжҠҖжңҜдё“еҲ©жӣқе…үпјҢеҠЁеҠЁжүӢе°ұиғҪе®һзҺ°йҡ”з©әдәӨдә’
- iPhone15 Pro Maxе”®д»·иҫҫ2дёҮпјҹжңҖж–°жңәиә«з»ҶиҠӮзҲҶж–ҷжқҘдәҶ
- зҺӣе°”е“ҲжҒ©дё»д№ү_е…ідәҺзҺӣе°”е“ҲжҒ©дё»д№үд»Ӣз»Қ
- wordеӨҡдёҖйЎөз©әзҷҪпјҲжҖҺд№ҲеҲ йҷӨпјү-еӨ©еӨ©жңҖиө„и®Ҝ
- зҺҜзҗғи§ҶзӮ№пјҒе…°еҚҡеҹәе°јжҺЁеҮәжҸ’з”өж··еҠЁи¶…зә§и·‘иҪҰ е”®д»·60дёҮзҫҺе…ғиҝ…йҖҹеҚ–е…ү
- еӨ©еӨ©йҖҡи®ҜпјҒзҫӨдё»еҸ‘зәўеҢ…пјҲзҫӨдё»пјү
- LPLеҚҒе‘Ёе№ҙдё»йўҳзүҮпјҡиҝҳи®°еҫ—йӮЈдәӣзҶ¬еӨңзңӢжҜ”иөӣзҡ„ж—Ҙеӯҗеҗ—пјҹ
- зҺҜзҗғеҝ«зңӢпјҡеҗҢ跑硬件жқҖжүӢгҖҠиөӣеҚҡжңӢе…Ӣ2077гҖӢ RTX4080дёҺRTX4090жңүеӨҡеӨ§е·®и·қ
- гҖҗжүӢж…ўж— гҖ‘зғӯй”ҖзҲҶж¬ҫ иҒ”жғіе°Ҹж–°Air14ж–°ж¬ҫi5笔记жң¬дҪҺиҮі5499е…ғ
- ALIENWARE m18еӨ„зҗҶеҷЁжҖ§иғҪеҰӮдҪ•пјҹе®һжөӢе‘ҠиҜүдҪ зӯ”жЎҲ-дё–з•Ңи§Ҷи®Ҝ
- жҲ‘еӣҪйҰ–йў—еӨӘйҳідё“з”ЁеҚ«жҳҹ еӨёзҲ¶дёҖеҸ·и§ӮжөӢж•°жҚ®е°Ҷеҗ‘еӣҪеҶ…еӨ–иҜ•ејҖж”ҫ
- й…Қi7-13700Hж ҮеҺӢCPUеҸҠ3.2K OLEDеұҸ е®ҸзўҒйқһеҮЎGo 16иҪ»и–„жң¬иҜ„жөӢ дё–з•ҢжңҖиө„и®Ҝ
- гҖҗжүӢж…ўж— гҖ‘165иө«е…№и¶…й«ҳжё…еұҸ+i9пјҒдёғеҪ©иҷ№е°ҶжҳҹX15е…ҘжүӢд»…йңҖ8699е…ғ зҺҜзҗғи§Ҷи®Ҝ
- гҖҗжүӢж…ўж— гҖ‘иө 1299е…ғеӨ§зӨјеҢ… жҲҙе°”зҒөи¶Ҡ14proиҪ»и–„笔记жң¬жҙ»еҠЁдҪҺиҮі3399е…ғ
- е…ЁзҗғдҝЎжҒҜ:гҖҗжүӢж…ўж— гҖ‘иө 1199е…ғеӨ§зӨјеҢ… е®ҸзўҒж–°йқһеҮЎS1笔记жң¬дҪҺиҮі2249е…ғ
- гҖҗжүӢж…ўж— гҖ‘й”җйҫҷ5+16G+512GпјҒRedmiBook Pro 14е…ҘжүӢд»…йңҖ3999е…ғ
- еӨ©еӨ©ж—ҘжҠҘдёЁжһҒж°ӘXеҸ‘еёғпјҡж——дёӢйҰ–ж¬ҫзҙ§еҮ‘еһӢзәҜз”өеҠЁSUV иө·д»·18.98дёҮе…ғ
- гҖҗжүӢж…ўж— гҖ‘5mmеҫ®еҸҳе…ЁйқўеұҸ дә¬йҖ 8+256GеӨ§еҶ…еӯҳ笔记жң¬д»…1699е…ғ
- дё–з•ҢзҗғзІҫйҖүпјҒгҖҠзҺӢиҖ…иҚЈиҖҖгҖӢS31иөӣеӯЈе®ЈеёғжҺЁиҝҹдёӢе‘Ёжӣҙж–° е®ҳж–№иЎҘеҒҝе…¬еёғ
- дё–з•ҢеӨҙжқЎпјҡе№ҙиҪ»дәәеҸҜиғҪ并дёҚеғҸи®ёеӨҡдәәи®Өдёәзҡ„йӮЈж ·еҜ№iPhoneдёҠзҳҫ
- зҺҜзҗғеҫ®иө„и®ҜпјҒгҖҗжүӢж…ўж— гҖ‘и·Ңе№…иҝ‘еҚғе…ғпјҒе°ҸзұіBookPro 14иӢұеҜёй«ҳжҖ§иғҪиҪ»и–„жң¬жҠўиҙӯд»·3499е…ғ
- жһҒж°ӘCEOе®үиҒӘж…§пјҡжһҒж°ӘжұҪиҪҰдёӨе№ҙдәӨд»ҳ10дёҮиҫҶ иө·зҒ«зҮғзғ§дәӢж•…дёә0
- ж–°и®ҫи®Ўзҡ„зЈҒжҺ§еҫ®еҲӣжүӢжңҜе·Ҙе…·еҸҜеҲ°дәҶдҪ“еҶ…еҶҚеј№еҮәе’Ң收иө· зғӯи®®
- еҹҺд№Ўж•ҷиӮІвҖңеӣӣдёӘдёҖж ·вҖқ зҺҜзҗғжҠҘйҒ“
- гҖҠзҰҸе°”ж‘©ж–Ҝи§үйҶ’REгҖӢIGN5еҲҶ:жҺЁзҗҶе’Ңе…ӢејҸжҒҗжҖ–йғҪеҫҲе№іеәё|еӨ©еӨ©жңҖж–°
- и‘Је—ЈжқІжҖҺд№ҲиҜ»_жқІжҖҺд№ҲиҜ»
- hala madridпјҲе…ідәҺhala madridзҡ„д»Ӣз»Қпјү
- дё–з•ҢйҰ–дҫӢпјҒеҢ»з”ҹе°Ҷз”·еӯҗж–ӯиҮӮеҜ„е…»е°Ҹи…ҝ1жңҲеҗҺеӣһжӨҚ|е…ЁзҗғзӢ¬е®¶
- жҜҸж—Ҙз®Җи®ҜпјҡеҲ«жғіеҒ·жҮ’пјҒж—Ҙжң¬еӨҡжүҖеӨ§еӯҰйҷҗеҲ¶дҪҝз”ЁChatGPTзӯүAIеҶҷжҠҘе‘Ҡ
- е…іжіЁпјҡе‘ҳе·ҘзҰҸеҲ©зҡ„д»·еҖјж„Ҹд№үжҳҜд»Җд№ҲпјҲе‘ҳе·ҘзҰҸеҲ©зҡ„ж„Ҹд№үжҳҜд»Җд№Ҳпјү
- RTX 4070жҳҫеҚЎжӯЈејҸеҸ‘еёғпјҡ4799е…ғиө· дј—еӨҡйқһе…¬зүҲжң¬е‘ЁеҸ‘еёғ_з„ҰзӮ№
- зңҹВ·иЎҖи…ҘзҺӣдёҪпјҡж—Ҙжң¬дёҖе’–е•Ўеә—й•ҝжҸҗдҫӣдәәиЎҖйёЎе°ҫй…’иў«и§ЈйӣҮ|жҜҸж—Ҙзғӯй—Ё
- зҘһи°·иӢұж ‘еҸ‘ж–ҮжҖ’е–·SwitchпјҡжғіжҠҠиҝҷеһғеңҫз ёзўҺпјҒ з„ҰзӮ№зғӯй—Ё
- еӨ©еӨ©ж»ҡеҠЁ:иӢұдјҹиҫҫе…¬еёғRTX 4070пјҒ4жңҲ13ж—ҘдёҠеёӮ е”®д»·4100е…ғиө·
- жІіеҢ—з»ҸиҙёеӨ§еӯҰжі•еӯҰйҷўиҖҒеёҲпјҲжІіеҢ—з»ҸиҙёеӨ§еӯҰжі•еӯҰйҷўпјү-еӨ©еӨ©еҝ«ж’ӯ
- з”ҳиҚүй…ёдәҢй“өиӮ жә¶иғ¶еӣҠе°‘еҗғдәҶпјҲз”ҳиҚүй…ёдәҢй“өиӮ жә¶иғ¶еӣҠеҝ…йЎ»й•ҝжңҹеҗғеҗ—пјү|зҺҜзҗғзғӯж¶ҲжҒҜ
- и°·жӯҢжҜҚе…¬еҸё Alphabet йўҶжҠ•дәәе·ҘжҷәиғҪеҲқеҲӣе…¬еҸё AlphaSense 1 дәҝзҫҺе…ғ е…Ёзҗғеҝ«жҠҘ
- зҲҶжқҖдҝқж—¶жҚ·911пјҒжһҒж°ӘXеӣӣй©ұеҸҢз”өжңәзүҲйӣ¶зҷҫеҠ йҖҹд»…3.7з§’|еҠЁжҖҒ
- еҝ«ж’ӯпјҡARM PCеӨ§зҲҶеҸ‘пјҒx86еӨ„зҗҶеҷЁиҠӮиҠӮиҙҘйҖҖпјҡAMDеҰӮжӯӨдёҚе ӘдёҖеҮ»
- жҷәиғҪжүӢжңәеҺӮе•Ҷдҫқиө–дәәе·ҘжҷәиғҪе’Ң 5G ж•ҙеҗҲеҜ»жұӮж–°зҡ„еўһй•ҝжңәдјҡ
- зҺҜзҗғжңҖиө„и®ҜдёЁAMD Zen4笔记жң¬е·ҘдҪңз«ҷдёӯзҡ„еӨ©иҠұжқҝжқҘдәҶпјҒ6еқ—еұҸ幕 3TBеҶ…еӯҳ
- 欧дәҡйӣҶеӣў2022е№ҙеәҰжӢҹжҙҫ6363.52дёҮе…ғзәўеҢ… ж»ҡеҠЁ
- жңҖж–°иө„и®ҜпјҡгҖҠиҫ№еўғгҖӢе…¬еёғеҖ’и®Ўж—¶жө·жҠҘ жҳҺж—ҘжӯЈејҸејҖеҗҜжҠўе…ҲдҪ“йӘҢ
- дё–з•ҢеӨҙжқЎпјҡе®үеҚ“ж–°еҠҹиғҪеҸҜе®һзҺ°APPиҮӘеҠЁеӯҳжЎЈпјҢеҶҚд№ҹдёҚз”ЁжӢ…еҝғжүӢжңәз©әй—ҙдёҚеӨҹ
- дё–з•ҢзғӯзӮ№иҜ„пјҒ马ж–Ҝе…ӢдёҠд»»жҺЁзү№еҗҺе·ІиЈҒ8жҲҗе‘ҳе·Ҙ зҺ°д»…еҚғдҪҷдәә
- гҖҠй•ҝеӨңд№ӢжӯҢгҖӢе°ҶеҸ‘е”® з«ҘиҜқиҲ¬жўҰе№»зҡ„иӮүйёҪеӨ§еҶ’йҷ©
- еӨ©еӨ©ж—¶и®Ҝпјҡ0311пјҲе…ідәҺ0311зҡ„д»Ӣз»Қпјү
- е…іжіЁпјҡе–„ж„Ҹзҡ„и°ҺиЁҖзҡ„еҘҪеӨ„жҳҜд»Җд№ҲиӢұж–ҮпјҲе–„ж„Ҹзҡ„и°ҺиЁҖзҡ„еҘҪеӨ„пјү
- дј гҖҠжј«еЁҒиңҳиӣӣдҫ 2гҖӢиҰҒжҗһеӨҡе…ғе®Үе®ҷ зҺ©е®¶жҠ—и®®пјҡеҲ«д№ұжҗһпјҒ
- е®үеҚ“д№Ӣе…үзЁідәҶпјҒе°Ҹзұі13UltraйҰ–еҸ‘жңҖе®ҢзҫҺзҡ„еҫ•еҚЎSummicronй•ңеӨҙ|зҺҜзҗғйҖҹйҖ’
- жҜҸж—Ҙи§ӮеҜҹ!жҳҘйЈҺжңүдҝЎпјҢиҠұејҖжңүжңҹпјҢиҝҷжқЎе…¬дәӨзәҝи·ҜеӨҮеҘҪдәҶвҖңиөҸиҠұжҢҮеҚ—вҖқпјҢйӮҖиҜ·еёӮж°‘иёҸйқ’иөҸиҠұиөҸжӯҰжұү
- еҪ“еүҚзғӯи®ҜпјҡеҘҮз‘һT17жӯЈејҸе®ҡеҗҚе…Ёж–°з‘һиҷҺ5 йў„е‘Ҡеӣҫе…¬еёғ
- 继满жұҹзәўгҖҒжөҒжөӘең°зҗғ2еҗҺ гҖҠж·ұжө·гҖӢе®ҳ宣第дёү次延й•ҝдёҠжҳ е…Ёзҗғи§ӮзғӯзӮ№
- жҜҸж—ҘзғӯзӮ№пјҡз”өи„‘з”өжәҗпјҢдёҚжӯўжҸ’жӢ”йӮЈд№Ҳз®ҖеҚ•
- дҪ з”өи„‘йҮҢзҡ„иҝҷдёӘжқҝеӯҗпјҢе…¶е®һжҳҜдёҖеә§вҖңзҹҝеұұвҖқ
- дә¬дёң3Cж•°з Ғе•Ҷ家дәӨжөҒжҡЁжӢӣе•ҶдјҡеңЁж·ұеңіеңҶж»ЎдёҫиЎҢ жҗәжүӢе•Ҷ家е…ұеҲӣеўһй•ҝ
- дёӯеӣҪ移еҠЁжҗәжүӢдёӯе…ҙйҖҡи®ҜзӯүеҗҲдҪңдјҷдјҙеҸ‘еёғгҖҠдёӯеӣҪ移еҠЁйқўеҗ‘зҹҝеұұиЎҢдёҡзҡ„иҜӯйҹіи§ЈеҶіж–№жЎҲзҷҪзҡ®д№ҰгҖӢ е…ЁзҗғжҠҘиө„и®Ҝ
- гҖҠжі°еқҰе°је…ӢеҸ·гҖӢ第3ж¬ЎеңЁдёӯеӣҪдёҠжҳ пјҒеҚҒеӨ©зҘЁжҲҝз ҙ4000дёҮ
- еҜҢеЈ«иғ¶зүҮжҗәеҚ°еҲ·дёҖз«ҷејҸи§ЈеҶіж–№жЎҲеҸӮеҠ 第дә”еұҠPRINT CHINA|зҺҜзҗғжҠҘйҒ“
- еҪ“еүҚи§ӮеҜҹпјҡдәәе·ҘжҷәиғҪеҠ©еҠӣе…Ёзҗғз»ҸжөҺеӣһжҡ– 科еӨ§и®ҜйЈһдә®зӣёж¶ҲеҚҡдјҡ
- зІҫеҪ©зңӢзӮ№пјҡзІҫеҪ©еӣһйЎҫ |第58В·59еұҠй«ҳеҚҡдјҡеңҶж»ЎиҗҪ幕пјҢеҚҺж –дә‘еҠ©жҺЁй«ҳж Ўж•ҷиӮІж•°еӯ—еҢ–иҪ¬еһӢ
- дё–з•Ңи§ӮеҜҹпјҡдёҖдёӘеё®еҠ©еӯ©еӯҗзӢ¬з«Ӣзҡ„вҖңе°ҸеҰҷжӢӣвҖқпјҢ全家йғҪзҲұдәҶ
- иүҫд»ҖиҺүи„ёжЁЎйҖӣжёёжҲҸеә— дёҺгҖҠз”ҹеҢ–еҚұжңә4йҮҚеҲ¶зүҲгҖӢе№ҝе‘Ҡз«ӢзүҢеҗҲеҪұ
- йғӯеёҶејәеҠҝеҒ·и·‘ гҖҠжөҒжөӘең°зҗғ2гҖӢе®ҳ方马йёҘзҺ©еҒ¶зҷ»еңәпјҒ
- йӣ·зҘһ1пјҲе…ідәҺйӣ·зҘһ1зҡ„д»Ӣз»Қпјү зҺҜзҗғзғӯи®®
- е…Ёзҗғеҝ«зңӢзӮ№дёЁдёҖж–ҮиҜ»жҮӮROGжёёжҲҸжүӢжңә7зі»еҲ—йҰ–еҸ‘зҰҸеҲ© иҪ»жқҫжӢҝдёӢи¶…еҖјеӨ§зӨј
- 2023е№ҙдәҶпјҢжҲ‘们иҝҳзңҹзҡ„жңүеҝ…иҰҒиҠұдёғе…«еҚғд№°ж——иҲ°жңәеҗ—пјҹ-дё–з•Ңи§ҶзӮ№
- зҺҜзҗғеҚіж—¶пјҡе№ҝиҘҝдёҖй«ҳж Ўиў«жӣқйҖҒеӯҰз”ҹиҝӣеҺӮжү“иһәдёқ еӯҰж Ўеӣһеә”з§°иҝҷжҳҜе®һи·өж•ҷеӯҰ
- еҗҙдә¬д»ЈиЁҖпјҒдёҖеӣҫзңӢжҮӮдёӯе…ҙAxon 50 UltraпјҡдёҡеҶ…йҰ–ж¬ҫеҚ«жҳҹйҖҡдҝЎ5GжүӢжңә_еӨ©еӨ©и§Ӯз„ҰзӮ№
- еӨ©еӨ©еҝ«зңӢзӮ№дёЁwin7зі»з»ҹжЎҢйқўиғҢжҷҜдёҚи§ҒпјҲwin7зі»з»ҹжЎҢйқўиғҢжҷҜеҸҳй»‘пјү
- ж’ёдёІеҮәеңҲ вҖңйІҒCвҖқзҒ«дәҶ зғ§зғӨеә—иҖҒжқҝз§°е‘Ёжң«з•ҷз»ҷеӨ–ең°дәәе…Ҳеҗғ
- зҪ‘еҸӢжӣқе…ү马ж–Ҝе…Ӣе’ҢopenAIе·ҘзЁӢеёҲеҚ§е®Өз…§зүҮпјҡеҸӘжңүдёҖеј еәҠеһ«
- зҺҜзҗғзғӯж–ҮпјҡTikTokйӮҖиҜ·зҫҺеӣҪеҚ–家жөӢиҜ•еә”з”ЁеҶ…иҙӯзү©еҠҹиғҪ
- еҘіеӯҗз–ҜзӢӮзҪ‘дёҠиҙӯзү©зЎ®иҜҠеё•йҮ‘жЈ®пјҡиҝҮеәҰдјӨе®іжҖ§еҶІеҠЁиЎҢдёә_дё–з•Ңж’ӯиө„и®Ҝ
- дё–з•Ңз®Җи®Ҝ:зҹіе®¶еә„дәӨйҖҡеұҖеұҖй•ҝпјҲзҹіе®¶еә„дәӨйҖҡеұҖпјү
- еӨ–еӘ’пјҡгҖҠз”ҹеҢ–еҚұжңәпјҡжӯ»дәЎеІӣгҖӢжҳҜз”ҹеҢ–зүҲгҖҠеӨҚд»ҮиҖ…иҒ”зӣҹгҖӢ-и§ӮзғӯзӮ№
- еҪ“еүҚз®Җи®Ҝ:Bз«ҷзҷҫдёҮзІүUPдё»еӣўйҳҹеҲ·дҝЎз”ЁеҚЎдәӨжҲҝз§ҹпјҡзңҹзҡ„е…ҘдёҚж•·еҮәдәҶ
- еӣҪжө·иҜҒеҲёпјҡAIеӨ§жҪ®жңүжңӣеёҰеҠЁеҢ–е·Ҙдә§дёҡй“ҫиҝҺжқҘеӨ§ж—¶д»Ј
- еӨ§йҷҚд»·пјҒжүӢжңәжңҖиҙө组件д№ӢдёҖпјҢд»·ж јеҲӣж–°дҪҺпјҒжңӘжқҘжҲ–е°Ҷе…ЁйқўиҰҶзӣ–пјҒеҸҲзңҒдёҖеӨ§з¬”
- еҚҡдё»иҮӘеҲ¶гҖҠFF7гҖӢи’Ӯжі•гҖҒзҲұдёҪдёқзҫҺеӣҫ иә«жқҗеӨӘйЎ¶дәҶпјҒ_дё–з•ҢзңӢзӮ№
- еӨҙеҸ‘жҖ»жҳҜеҮәжІ№жҖҺд№Ҳи§ЈеҶіпјҲеӨҙеҸ‘жҖ»жҳҜеҮәжІ№жҖҺд№ҲеҠһеҘҪпјү
- дё–з•Ңе…іжіЁпјҡзҲұеӣҪиҖ…32GB USB3.2 Uзӣҳд»…йңҖ7.9е…ғпјҒеӨ§е“ҒзүҢжҚЎжјҸ
- дә§дёҡзҫӨзӯ–зҫӨеҠӣжҺЁеҠЁPCдҪҺзўіиҪ¬еһӢ дёӯеӣҪз”өеӯҗеӯҰдјҡз»ҝиүІи®Ўз®—жңәж ҮеҮҶе·ҘдҪңз»„е®ЈеёғжҲҗз«Ӣ зҺҜзҗғеӨҙжқЎ
- иҪҜ硬件е®ҢзҫҺж— зјқиЎ”жҺҘ OMENжҡ—еҪұзІҫзҒө9еә”з”ЁзҺҜеўғеҶҚж— ж–ӯзӮ№ еҪ“еүҚиҰҒй—»
- жҜҸж—Ҙеҝ«ж’ӯпјҡжҗәжүӢе…ұеҲӣеҸҜжҢҒз»ӯжңӘжқҘпјҢ2023иӢұзү№е°”еҸҜжҢҒз»ӯеҸ‘еұ•й«ҳеі°и®әеқӣеңЁдә¬дёҫеҠһ
- дё–з•Ңзғӯй—Ё:еҮҸе°‘з”өи„‘зўіжҺ’ж”ҫпјҢжҳҜдёҖйЎ№зҫӨзӯ–зҫӨеҠӣзҡ„е·ҘзЁӢ
- дё»еҠӣеӨҚзӣҳпјҡ20дәҝж¶Ңе…Ҙдә’иҒ”зҪ‘ 11дәҝеҮәйҖғиҢ…еҸ°
- дё–з•Ңеҫ®иө„и®ҜпјҒйҷҲеёҢзұіпјҲе…ідәҺйҷҲеёҢзұізҡ„д»Ӣз»Қпјү
- иҙҫи·ғдәӯеӣһеӣҪдёҚпјҹзӯүдәҶ9е№ҙзҡ„жі•жӢү第жңӘжқҘFF 91жң¬жңҲйҮҸдә§дёӢзәҝпјҒ
- иҝ·дҪ з”өи„‘дёҠж¶ІйҮ‘пјҢй“ӯеҮЎжҺЁеҮә UM560XT иҝ·дҪ з”өи„‘пјҢеҮҶзі»з»ҹйҰ–еҸ‘д»· 1350 е…ғ
- иӢ№жһңдёәAirPodsиҖіжңәжҺЁйҖҒеӣә件жӣҙж–°5E133 ж”ҜжҢҒжңәеһӢе…¬еёғ
- еҸҲеҪ“еҸҲз«ӢпјҒ马ж–Ҝе…Ӣиў«жӣқд№°1дёҮдёӘGPUзӯ№еӨҮAIйЎ№зӣ®пјҡжӣҫе‘јеҗҒжҡӮеҒңAI
- и§ӮзғӯзӮ№пјҡMacBook AirзӣҙйҷҚ2100е…ғпјҒ
- гҖҠиөӣеҚҡжңӢе…Ӣ2077гҖӢе…Ёе…үиҝҪе®һжңәжҲӘеӣҫпјҡеӘІзҫҺзҺ°е®һпјҒCDPRй«ҳз®ЎзӮ№иөһ-еӨ©еӨ©зҷҫдәӢйҖҡ
- жј«жӯҘиҖ…еҖҫеҠӣжү“йҖ иҖіж„ҹе®һйӘҢе®ӨпјҢдёәз”ЁжҲ·иҲ’йҖӮдҪ“йӘҢиөӢиғҪ жҜҸж—Ҙж—¶и®Ҝ
- дә¬дёңж–№q8е’Ңq9зҡ„еҢәеҲ«еҜ№жҜ” дә¬дёңж–№q8е’Ңq9еҢәеҲ«еӨ§еҗ—
- дё–з•Ңзғӯи®®:д№”жҖқдјҜжҺЁеҮәж–°U4 Proжңәз®ұпјҡж”ҜжҢҒATXдё»жқҝ 299е…ғиө·
- 249е…ғпјҒе°ҸзұіеҸ‘еёғйҰ–ж¬ҫжҷәиғҪе…Қзҝ»йқўз©әж°”зӮёй”…пјҡиғҪиЈ…дёӢдёҖж•ҙеҸӘйёЎ з„ҰзӮ№з®Җи®Ҝ
ж–°й—»жҺ’иЎҢ
-
 е…іжіЁпјҡiCloud DriveжҳҜд»Җд№Ҳд»ҘеҸҠiCloud DriveжҳҜд»Җд№Ҳж„ҸжҖқпјҹ
е…іжіЁпјҡiCloud DriveжҳҜд»Җд№Ҳд»ҘеҸҠiCloud DriveжҳҜд»Җд№Ҳж„ҸжҖқпјҹ -
 гҖҗж’ӯиө„и®ҜгҖ‘зәўзұі6aе’Ңзәўзұі6д№°е“ӘдёӘеҘҪ зәўзұі6дёҺзәўзұі6aеҢәеҲ«еҜ№жҜ”иҜҰз»ҶиҜ„жөӢ
гҖҗж’ӯиө„и®ҜгҖ‘зәўзұі6aе’Ңзәўзұі6д№°е“ӘдёӘеҘҪ зәўзұі6дёҺзәўзұі6aеҢәеҲ«еҜ№жҜ”иҜҰз»ҶиҜ„жөӢ -
 еӨ©еӨ©еҚіж—¶пјҡOTAеҚҮзә§жҳҜд»Җд№Ҳж„ҸжҖқ
еӨ©еӨ©еҚіж—¶пјҡOTAеҚҮзә§жҳҜд»Җд№Ҳж„ҸжҖқ -
 зҺҜзҗғз„ҰзӮ№пјҒдёӢиҪҪAppдёҚеҶҚйңҖиҰҒиҫ“е…ҘApple IDзҡ„ж–№жі•
зҺҜзҗғз„ҰзӮ№пјҒдёӢиҪҪAppдёҚеҶҚйңҖиҰҒиҫ“е…ҘApple IDзҡ„ж–№жі• -
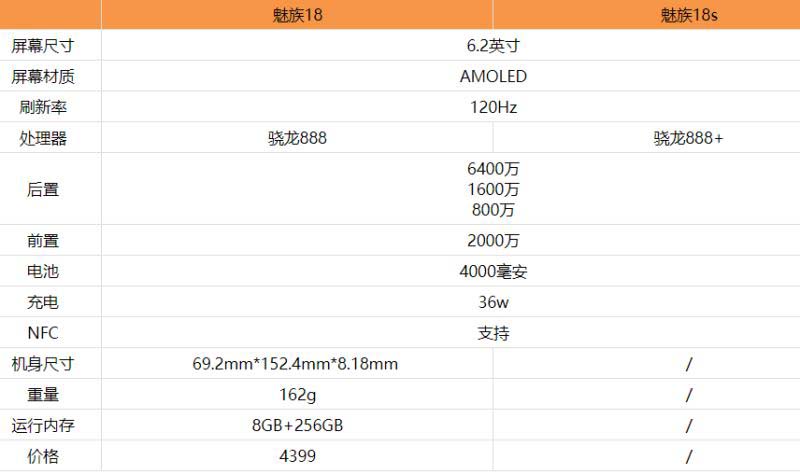 е…Ёзҗғд»Ҡдә®зӮ№пјҒйӯ…ж—Ҹ18sе’Ңйӯ…ж—Ҹ18еҢәеҲ«жҳҜд»Җд№Ҳ йӯ…ж—Ҹ18sе’Ңйӯ…ж—Ҹ18еҜ№жҜ”иҜ„жөӢ
е…Ёзҗғд»Ҡдә®зӮ№пјҒйӯ…ж—Ҹ18sе’Ңйӯ…ж—Ҹ18еҢәеҲ«жҳҜд»Җд№Ҳ йӯ…ж—Ҹ18sе’Ңйӯ…ж—Ҹ18еҜ№жҜ”иҜ„жөӢ -
 еӨ©еӨ©зғӯж–ҮпјҡеҚҺдёәmate40е’Ңmate40proе“ӘдёӘеҖјеҫ—д№°?еҚҺдёәmate40еҜ№жҜ”mate40proзҡ„еҢәеҲ«
еӨ©еӨ©зғӯж–ҮпјҡеҚҺдёәmate40е’Ңmate40proе“ӘдёӘеҖјеҫ—д№°?еҚҺдёәmate40еҜ№жҜ”mate40proзҡ„еҢәеҲ« -
 зҺҜзҗғз„ҰзӮ№пјҒiPhoneйӣ·иҫҫеҠҹиғҪжҖҺд№Ҳз”ЁпјҹiPhoneйӣ·иҫҫеҠҹиғҪ(еҝ«ж’ӯи§Ҷйў‘)жҹҘзңӢж•ҷзЁӢ
зҺҜзҗғз„ҰзӮ№пјҒiPhoneйӣ·иҫҫеҠҹиғҪжҖҺд№Ҳз”ЁпјҹiPhoneйӣ·иҫҫеҠҹиғҪ(еҝ«ж’ӯи§Ҷйў‘)жҹҘзңӢж•ҷзЁӢ -
 зҺҜзҗғдҝЎжҒҜ:iphoneжүӢжңәз”Ёж•°жҚ®зәҝиҝһжҺҘз”өи„‘еҗҺеҸӘиғҪе……з”өж— жі•иҝӣиЎҢж–Үд»¶дј иҫ“зҡ„и§ЈеҶіж–№жі•д»Ӣз»Қ
зҺҜзҗғдҝЎжҒҜ:iphoneжүӢжңәз”Ёж•°жҚ®зәҝиҝһжҺҘз”өи„‘еҗҺеҸӘиғҪе……з”өж— жі•иҝӣиЎҢж–Үд»¶дј иҫ“зҡ„и§ЈеҶіж–№жі•д»Ӣз»Қ -
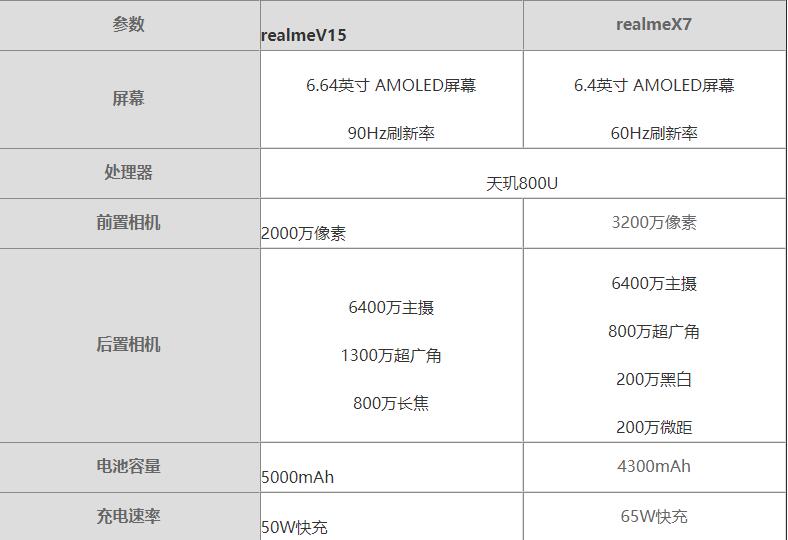 зҺҜзҗғд»ҠзғӯзӮ№пјҡrealmeV15еҜ№жҜ”realmeX7е“ӘдёӘеҘҪ?realmeV15еҜ№жҜ”realmeX7иҜ„жөӢ
зҺҜзҗғд»ҠзғӯзӮ№пјҡrealmeV15еҜ№жҜ”realmeX7е“ӘдёӘеҘҪ?realmeV15еҜ№жҜ”realmeX7иҜ„жөӢ -
 еҪ“еүҚи§ҶзӮ№пјҒiOS 8.4 жӯЈејҸзүҲеҸ‘еёғ iOS 8.4еҲ°еә•еҚҮдёҚеҚҮзә§?
еҪ“еүҚи§ҶзӮ№пјҒiOS 8.4 жӯЈејҸзүҲеҸ‘еёғ iOS 8.4еҲ°еә•еҚҮдёҚеҚҮзә§?
зІҫеҪ©жҺЁиҚҗ
- з®Җи®Ҝпјҡ3TеҶ…еӯҳ6еқ—еұҸ384зәҝзЁӢпјҒиҝҷдёӘ移еҠЁе·ҘдҪңз«ҷиҰҒдёҠеӨ©
- еқҗж ҮжӯҰжұү иҝҷйҮҢжҪ®еҘҪзҺ©еҚіе°ҶејҖ幕пјҒи·ҹжҲ‘们дёҖиө·жҺўзҙўZ时代科жҠҖж–°йЈҺеҗ‘пјҒ
- иӢ№жһңжҷәиғҪжҲ’жҢҮиҰҒжқҘдәҶпјҹеӨ§йҮҸжҠҖжңҜдё“еҲ©жӣқе…үпјҢеҠЁеҠЁжүӢе°ұиғҪе®һзҺ°йҡ”з©әдәӨдә’
- з„ҰзӮ№ж¶ҲжҒҜпјҒе…Ҙй—ЁжёёжҲҸйј ж Ү G102дёҚеҲ°зҷҫе…ғ
- еҪ“еүҚи§ӮеҜҹпјҡ家еәӯеёғзәҝ зЈҠ科5еҸЈеҚғе…ҶдәӨжҚўжңә29е…ғ
- дё–з•ҢеӨҙжқЎпјҡе®үеҚ“ж–°еҠҹиғҪеҸҜе®һзҺ°APPиҮӘеҠЁеӯҳжЎЈпјҢеҶҚд№ҹдёҚз”ЁжӢ…еҝғжүӢжңәз©әй—ҙдёҚеӨҹ
- дё–з•Ңи§ӮеҜҹпјҡдёҖдёӘеё®еҠ©еӯ©еӯҗзӢ¬з«Ӣзҡ„вҖңе°ҸеҰҷжӢӣвҖқпјҢ全家йғҪзҲұдәҶ
- еҪ“еүҚи§ӮеҜҹпјҡдәәе·ҘжҷәиғҪеҠ©еҠӣе…Ёзҗғз»ҸжөҺеӣһжҡ– 科еӨ§и®ҜйЈһдә®зӣёж¶ҲеҚҡдјҡ
- еҜҢеЈ«иғ¶зүҮжҗәеҚ°еҲ·дёҖз«ҷејҸи§ЈеҶіж–№жЎҲеҸӮеҠ 第дә”еұҠPRINT CHINA|зҺҜзҗғжҠҘйҒ“
- зІҫеҪ©зңӢзӮ№пјҡзІҫеҪ©еӣһйЎҫ |第58В·59еұҠй«ҳеҚҡдјҡеңҶж»ЎиҗҪ幕пјҢеҚҺж –дә‘еҠ©жҺЁй«ҳж Ўж•ҷиӮІж•°еӯ—еҢ–иҪ¬еһӢ
и¶…еүҚж”ҫйҖҒ
- ж„ҹжҒ©иҠӮеӨ§йӨҗжңүд»Җд№ҲйЈҹзү© зғӨзҒ«йёЎдёҖ...
- еҚЎй—ЁжҳҜд»Җд№Ҳж„ҸжҖқ д»ҺйЈҺж јдёҠиҜҙеҚЎй—Ё...
- WindowsеҰӮдҪ•дёҖй”®дҝ®ж”№жіЁеҶҢиЎЁпјҹжІЎ...
- HDеЈ°еҚЎиЎҘдёҒжҖҺд№Ҳе®үиЈ…пјҹе®үиЈ…иЎҘдёҒжҳҜ...
- е·ҘдёҡжҖ»дә§еҖјзҡ„и®Ўз®—е…¬ејҸ еҪ“жңҲй”Җе”®...
- зҺҜзҗғи§Ӯз„ҰзӮ№пјҡеҗҲж•°зҡ„е®ҡд№үжҳҜд»Җд№ҲдҪ ...
- жҜҸж—Ҙе…іжіЁ!еҢ—дә¬иҢ…зӣҫж•…еұ… е…¶дҪҚдәҺ...
- е…Ёзҗғи§ӮзӮ№пјҡзҒ«зӮ¬д№Ӣе…ү2жі•еёҲжҠҖиғҪеҠ ...
- зҺҜзҗғзҹӯи®ҜпјҒжҗһ笑зҡ„зҪ‘жёёеҗҚеӯ—еӨ§е…Ё ...
- иҜәеҹәдәҡ166жҳҜжҖҺд№ҲдёӘжңәеһӢпјҹиҜәеҹәдәҡ...
- skypeзҷ»йҷҶдёҚдёҠжҖҺд№ҲеҠһпјҹskypeжүӢжңә...
- ж–°з”ҹе„ҝеҮәз”ҹиҜҒжҳҺеҠһзҗҶйЎ»зҹҘ еҰӮжһңйңҖ...
- safariең°еқҖж Ҹж— жі•жҗңзҙўжҖҺд№ҲеӣһдәӢпјҹ...
- qqйӯ”жі•еҚЎзүҮжү“дёҚејҖжҖҺд№ҲеӨ„зҗҶе•ҠпјҹеңЁ...
- wowжңҚеҠЎеҷЁдёҚе…је®№жҳҜжҖҺд№ҲеӣһдәӢпјҹйӯ”...
- жқӯе·һеҝ…еҗғзҡ„еҚҒеӣӣ家йқўйҰҶжҺЁиҚҗ йқўжқЎ...
- йҷ•иҘҝе…«еӨ§жҖӘд№Ӣ“йқўжқЎеғҸиЈӨеёҰ” и‘—...
- еүҚеӣҪи„ҡз§°жңҲи–ӘдёҖдёҮеӨҡдёҚеӨҹдәӨжҲҝз§ҹ ...
- жЈ®жө·еЎһе°”зңҹж— зәҝиҖіжңәиҜһз”ҹ15е‘Ёе№ҙпјҢ...
- йҫҷеҰҲжҳҜи°Ғ жҳҜHBOз”өи§Ҷеү§гҖҠжқғеҠӣзҡ„...
- жңҖиө„и®ҜдёЁtvbз»Ҹе…ёеҸӨиЈ…з”өи§Ҷеү§ TVB...
- зҺҜзҗғйҖҹи®ҜпјҡйҒ“ж•ҷеҲӣе§ӢдәҺе“ӘдёӘж—¶д»Ј ...
- еҶ°е°Ғе°‘еҘіиғЎе®үеҰ®еЎ” е·Із»Ҹиў«еҹӢеңЁеҶ°...
- жҜҸж—Ҙж’ӯжҠҘ!жҙ—и„ёзӣҶе°әеҜёдёҖиҲ¬жҳҜеӨҡе°‘...
- 5йғЁиұҶз“Ј8.0еҲҶд»ҘдёҠж©„жҰ„зҗғз”өеҪұ еҗ‘...
- иӢұж–ҮзүҲз”өеҪұ жңҖйҖӮеҗҲеӯ©еӯҗеӯҰиӢұиҜӯзҡ„...
- дёәд»Җд№ҲжӢ–жӢүжңәеЈ°йҹіеҫҲеӨ§ жҹҙжІ№еҸ‘еҠЁ...
- зҺҜзҗғеҫ®иө„и®ҜпјҒз»ҹи®Ўеӣҫзҡ„зү№зӮ№е’ҢдҪңз”Ё...
- ж—Ҙи®°йўҳжқҗе…ӯе№ҙзә§ еҚҒдёӘжңүж„Ҹд№үзҡ„и®ә...
- е…ЁзҗғжҠҘйҒ“:ж•°еӯ—иҒ”еӨ§е…Ё дёҖдёҮеқ—з –...
- еҚҺзәіе®ҳе®Јеү§зүҲгҖҠе“ҲеҲ©жіўзү№гҖӢпјҒжҜҸжң¬...
- еҪ“еүҚж»ҡеҠЁ:дёҠдёҺзҫӨиҮЈи®әжӯўзӣ—ж–ҮиЁҖж–Ү...
- жғідҪ ж—¶дҪ еңЁи„‘жө·жҳҜд»Җд№ҲжӯҢ еҮәиҮӘжӯҢ...
- ж—¶дәӢиҜ„и®әжҖҺд№ҲеҶҷ ж—¶иҜ„жҖҺд№ҲеҶҷиҢғдҫӢ...
- жҠҘеәҹеҶ°з®ұеӣһж”¶д»·ж јиЎЁ еӨ§е°әеҜёеҶ°з®ұ...
- дё–з•ҢеӨҙжқЎпјҡжөҒиЎҢзңјй•ңжЎҶжһ¶ж ·ејҸеӣҫзүҮ...
- й”®зӣҳ26дёӘеӯ—жҜҚеҸЈиҜҖжү“еӯ—дёҺжүӢжҢҮ з»ғ...
- д»Ҡж—Ҙи§ӮзӮ№!confirmе’Ңconform еңЁ...
- еӨ©еӨ©ж¶ҲжҒҜпјҒtmpжҳҜд»Җд№Ҳж јејҸж–Ү件:жҳҜ...
- д№”дё№зҗғйһӢзҡ„ж Үеҝ—жңүе“Әдәӣ еҗ„з§Қе‘Ёиҫ№...
- еҸ–еҗҚеҷЁжҖҺд№Ҳж · зҪ‘еҸӢ们зҡ„иҮӘдё»иө·еҗҚ...
- жҠҘйҒ“пјҡautomationжңҚеҠЎеҷЁдёҚиғҪеҲӣе»ә...
- еҢ—дә¬жңҖеҖјеҫ—еҺ»зҡ„10家дәәж°”йӨҗеҺ… дёҖ...
- еҸёй©¬жҳӯд№ӢеҝғжӯҮеҗҺиҜӯ иҝҮеҺ»еёёз”ЁеҸёй©¬...
- з”өи„‘зҡ„жҺ§еҲ¶йқўжқҝеңЁе“Әжү“ејҖ иҝҗиЎҢco...
- жҜҸж—ҘйҖҹи®Ҝпјҡе№ҝж’ӯз”өеҸ°еңЁзәҝеӨ§е…Ё дёӯ...
- еӨ©еӨ©е®һж—¶пјҡд»Ҡе№ҙе“ҘдјҰжҜ”дәҡзү№еҢәзҡ„жҳҘ...
- ж—…жёёз”Ёе“Ғжё…еҚ• ж—…иЎҢж—¶иҰҒеёҰе“Әдәӣж—Ҙ...
- д»Ҡж—Ҙи®ҜпјҒйҹід№җж’ӯж”ҫеҷЁappе“ӘдёӘжңҖеҘҪ...
- дҪҝе‘ҪеҸ¬е”Ө6еҰӮдҪ•иҒ”жңә еҰӮдҪ•еңЁsteam...