二重积分的几何意义 所以这个函数的具体表达式是什么
关于二重积分的几何意义(二重积分的几何意义是面积还是体积) 这个很多人还不知道,今天小编来为大家解答以上的问题,现在让我们一起来看看吧!
 【资料图】
【资料图】
今天和大家分享一下关于二重积分的几何意义的问题(二重积分的几何意义是面积还是体积)。以下是小编对这个问题的总结。让我们看一看。
一、二重积分的几何意义是什么?
二。二重积分的几何意义:
楼上解释错了。1、本题的被积函数是一个顶点在原点的圆锥体,不是圆柱体。
2、如果被积函数的量纲是长度单位,则二重积分为体积;
3、如果被积函数的量纲是Pa,则二重积分的意义为计算总压力;
4、如果被积函数的量纲是kg/m²,则二重积分的意义就是算总质量;
5、如果被积函数的量纲是C/m² ,则二重积分的意义就是算总电量;
、、、、、、
结论:
1、二重积分是否有意义,要看被积函数的量纲,由量纲决定是否有物理意义。
2、数学老师出题,一般不会考虑什么物理模型、量纲,一般均无明确意义。
3、对于数学老师随意出出来的二重积分题,笼统地讲是算体积,其实是错的。
4、被积函数如果是1,而且这个1不带任何单位,那二重积分就是算总面积。
5、只要被积函数不是1,一般来说,二重积分没有明确意义,只是乱积而已。
数学老师出出来的二重积分的题,一般都是为了练习、熟练积分而出的题,
不必认真,只是练习而已。如果你一旦认真起来,无论你的天赋多高,创
造力多强,无论数学老师多烂,都会骂你“钻牛角尖”,“脑子有问题”。天才
就当成了 *** 。
本题的解释:
1、因为本题的被积函数是圆锥体,假设x、y均有长度量纲,本题的被积函数
的意义是圆锥体上的任何一点,这一点到x-y平面的垂直高度;
2、这个高度乘以x-y平面上的微元面积dxdy,就是一个细高的立体体积,这个
细高立体的底面在x-y平面上,顶面在圆锥体的侧面上。
3、积分的结果就是圆锥体下方到x-y平面的立体体积。
4、这个体积正好等于以圆锥口为顶面,底面在x-y平面上的圆柱的体积,减去
圆锥的体积。也就是楼主题目所问的问题。
5、本题是特例,结果等于圆柱的体积减去圆锥的体积。一般情况下不是这样。
三。二重积分的几何意义
二重积分∫∫f(x,y)dxdy的几何意义是曲顶柱体的体积,其中柱体的底为积分区域d,顶为z=f(x,y)确定的曲面。本题中z=(a^2-x^2-y^2)表示球体x^2+y^2+z^2=a^2的上半部分,底面时xoy平面上的x^2+y^2=a^2,根据几何意义,积分等于这上半球体的体积=2πa^3/3。四。二重积分的几何意义是什么?
定积分的几何意义是有曲边梯形的有向面积,物理意义是变速直线运动的距离或变力所做的功。
二重积分的几何意义是曲顶圆柱体的有向体积,物理意义是施加在平面面积上的压力(变压)。
积分的线性性质;
性质1(积分可加性)函数的和(差)的二重积分等于每个函数的二重积分的和(差)。
2.性质(积分满足数乘)的被积函数的常系数因子可称为积分外可比性:
3性质若在区域D中存在f(x,y)≦g(x,y)估计量:性质4设m和m为函数f(x,y)在有界闭区域D中的更大值和最小值,σ为区域D的面积性质5若f(x,y)=k(k为常数)在有界闭区域D中,σ为D的面积。
二重积分中值定理:设函数f(x,y)在有界闭区域D上连续,σ为该区域的面积,则D上至少有一个点(ξ,η)。
溶液法
二重积分和定积分一样,不是函数,而是数值。所以,如果一个连续函数f(x,y)包含一个二重积分,这个二重积分的具体值可以通过对它进行二次积分来求解。
积分区域d是由。
其中二重积分为常数,设它为a .对方程两端D的积分面积做二重定积分。
所以这个函数的具体表达式是:f(x,y)=xy+1/8,方程的右边是二重积分值为A,而方程最左边的部分可以根据性质5转化为常数A乘以积分面积的1/3,含有二重积分的方程可以转化为未知的A来求解。
设ω是空之间的有界闭区域,f(x,y,z)在ω上连续。
(1)如果ω关于xOy(或xOz或yOz)对称且f(x,y,z)是关于z(或y或x)的奇函数
(2)若ω关于xOy(或xOz或yOz)对称,则ω 1是ω在对应坐标平面一侧的部分,f(x,y,z)是关于z(或y或x)的偶函数
(3)如果ω和ω’关于平面y=x对称
以上小编是二重积分的几何意义(二重积分的几何意义是面积还是体积)及相关问题的解答。希望二重积分的几何意义(二重积分的几何意义是面积还是体积)这个问题对你有用!
\- 端午节的顺口溜以及儿歌童谣都写了什么 让我们来看看|环球聚焦
- 钢丝绳电动葫芦参数 电动葫芦有哪些规格型号?非标准电动葫芦是什么意思
- 前沿热点:掌阅科技:正接入市场主流AI大模型
- premiere加字幕教程 默认的静态字幕菜单是怎么调用出来的|独家
- Meta提出新模型MegaByte 可增强AI生成
- 穿越沙漠和自由是哪本书里的:纳尼亚传奇1-9章概要 世界今头条
- 新消息丨肉鸡病毒 本文将对鸡病毒性疾病的治疗方法进行深入的探讨
- 英雄联盟6300英雄推荐 官方说佐伊这个英雄的入门难度只有5可信吗|每日速读
- 春天在哪里串词是什么意思 那么这件事究竟是怎么发生的呢?
- 建设银行收入证明范本图片_建设银行收入证明范本
- 今日最新!姥姥的剪纸课文 如何用具体的语言素材感受奶奶的别出心裁
- 不可思议之国的冒险酒馆 炉石传说也如愿推出了新的冒险模式-全球热推荐
- 【世界速看料】那年青春我们正好:主题曲是由歌手章雷、作词人、作曲家共同演唱
- 男生耗时2周自制游戏必修教材书:《原神》启动!
- 天天报道:前5月A股市场融资总额超5000亿元公用事业行业融资总额居首
- 焦点简讯:研报掘金丨信达证券:旭升集团再获优质客户大额定点,加快全球化业务布局维持“买入”评级
- 焦点关注:上海迪士尼高峰日价格涨至799元!开园7年涨价4次
- 列阵沧海练攻防丨海军某中心海上训练掠影
- 菩提子手串怎么盘玩效果最好(菩提子手串怎么盘)
- 建党伟业国语高清下载链接(建党伟业高清下载)
- 巴萨发布对神户胜利船海报:稍后见,伊涅斯塔 世界头条
- 基金调研丨大成基金调研世华科技
- 全球视点!【手慢无】618特惠!华硕天选4 15.6英寸笔记本电脑光追独显降300元!
- 沪深股通|鄂尔多斯6月5日获外资卖出0.02%股份|全球视讯
- 环球热头条丨每月额度升至2000元 北京进一步优化租房提取公积金业务
- 苹果iOS 17正式发布:可自动清除短信验证码|环球关注
- 一次抽到荣耀水晶教程_抽到荣耀水晶的窍门
- 最后一分钟的谣言称苹果的AR耳机价格将大大低于3000美元
- 海利得:6月5日获融资买入257.13万元,占当日流入资金比例8.02% 环球速读
- 不用再说“嘿 Siri”了,iOS17新变化一文汇总
- 我国首个生物育种领域技术创新中心在内蒙古兴安盟获批
- 是校园也是图书馆 北京市青少年学生读书行动启动 当前快看
- 任天堂会员游戏库更新!追加《滚滚卡比》等4款游戏
- 世界最新:猎人t20套装(猎人t2套装)
- 焦点消息!美服eShop开启卡普空40周年特惠 多款游戏新史低!
- iPhone可碰一碰传输了!发送邮件账号、电话号码等-环球焦点
- 小学生体质测试标准_小学生体质健康标准|全球观点
- 青山纸业(600103.SH):不涉及Chatgpt业务 全球视点
- 海通证券:拟启动“基于金融大语言模型的证券公司内部协同助手”课题研究_世界即时看
- 当前观点:英雄联盟cdkey怎么获得(lolcdkey怎么获得)
- 淮南市潘集区平圩镇:“三化联动”激活电教远教“一池春水”-环球播报
- 6月6日 11:25分 正元地信(688509)股价快速拉升
- 全球观点:【手慢无】到手仅6199元!MacBook Air开始甩货了
- 【手慢无】618限时促销!华硕无畏Pro15跌破5000|天天观速讯
- 【手慢无】再降400元!ThinkBook 16+价格已触底 环球看点
- 消灭臭虫的最好药_消灭臭虫的最佳办法 资讯
- 全球观点:【手慢无】4060满血游戏本价格太香了!暗影精灵9跌至6679元
- 【手慢无】R7-7840HS强芯 机械革命无界14+笔记本跌至3799元
- 国内商品期货开盘涨跌不一黑色系涨幅居前
- 世界快资讯:【在希望的田野上】全国麦收过四成
- 全球新资讯:【手慢无】首发价再降120元!惠普暗影精灵9价格太馋人
- 当前快报:裕兴股份:高端光学聚酯基膜生产线已开始调试试生产
- 日本政府计划投资15万亿日元普及氢能-关注
- 《后来的人类》:写普通人的科幻小说,写出技术时代张爱玲的感觉 播报
- 传3B家居(BBBYQ.US)正就出售旗下婴儿用品连锁店进行谈判
- 宫颈癌手术后能吃枇杷吗 天天快资讯
- 永远在重启 真人《蝙蝠侠与罗宾》将选新任蝙蝠侠 环球信息
- 全球观点:这个世界需要英雄,但如果他们已经忘记了初衷呢?
- 网站泄密《原神》新版本:遭米哈游索赔百万!
- 要闻速递:AI马斯克婴儿照又萌又怪
- 焦点报道:吉安绿能联合体3.73亿竞得南昌经开91.3亩地结果无效 并被列入失信“黑名单”
- 当前看点!小鸡宝宝考考你在中国空间站生活的宇航员,他们能用Wi-Fi吗
- 世界讯息:什么是光纤宽带上网(什么是光纤)
- 头条焦点:《C++并发编程实战》读书笔记(1):并发、线程管控
- DC新片《蓝甲虫》发布新剧照:拉丁超英战斗模式开启!|焦点热闻
- 快报:苹果Mac三大新品价格汇总:最贵接近10万
- 环球观焦点:15英寸MacBook Air国内价格出炉:10499元起
- 关注世界环境日丨建设人与自然和谐共生的美丽河南 河南亮出“环保成绩单”
- 文物里的二十四节气·芒种_当前速看
- 苹果Mac Studio发布:M2 Ultra最强芯片版32999元起_速看
- QQ空间迎来18周年生日 称新功能亲密空间即将上线 快看
- iOS 17支持机型名单发布:iPhone X无缘
- 【全球报资讯】日本横须贺市试用结果良好后 在行政工作正式采用 ChatGPT
- 半藏森林克隆人暂下线 内测名额已满所以先下线了_天天新资讯
- 【世界新要闻】库克 今年将是最精彩WWDC 让我们码出新宇宙
- 当前快讯:苹果发布史上最大全球最轻15寸笔记本:价格破万
- 英特尔将出售部分Mobileye股票 可筹集约15亿美元资金|环球新消息
- 德国政府签订合同 携手航天初创公司Polaris开发Linear AeroSpike太空引擎 天天快资讯
- 21个行业获融资净买入 电子行业获净买入最多|环球新资讯
- 诗意中国丨趁晴割麦收云黄
- 让大学生村医扎根农村、茁壮成长 环球新视野
- wp7系统为何不能升级wp8(wp7系统)
- 昌江:12345热线搭上创文直通车 “接诉即办”解民忧
- 每日热文:职校有哪些专业适合初中学历男生(职校有哪些专业)
- 10:28 中字头个股异动拉升,中国出版2连板
- 《封神第一部》官宣定档7月20日!定档预告公布 环球热推荐
- 世界观天下!让大学生村医扎根农村、茁壮成长
- 苹果AirPods耳机新增自适应音频功能 减少周围噪音_环球看点
- iPhone不用再说“嘿 Siri”了!用户担忧误唤醒
- AI生成马斯克婴儿照被疯传 本人回应 返老还童药吃多了|天天头条
- 《最终幻想16》全新截图 画面绚丽角色逼真
- 世界快报:临泉县兴业路实验学校举办校园文化艺术节暨庆六一文艺会演
- 唯品会崩了相关负责人被免职 影响客户达800多万
- 哪里有快手小店通运营开户_快手小店通运营开户指南|世界通讯
- 国际金价短期或陷区间震荡
- 15英寸MacBook Air售价破万|天天快资讯
- 当前动态:不用再说“嘿 Siri”了 直接“Siri”即可唤醒语音助手
- 苹果MR头显Vision Pro敢卖25000元!
- 环球快资讯:618狂降800元:不到8000元入手惠普VICTUS光影精灵9 这波福利机不可失
- 天天观天下!解决MR头显软件生态难题:苹果将推出Vision Pro开发者套件
新闻排行
-
 关注:iCloud Drive是什么以及iCloud Drive是什么意思?
关注:iCloud Drive是什么以及iCloud Drive是什么意思? -
 【播资讯】红米6a和红米6买哪个好 红米6与红米6a区别对比详细评测
【播资讯】红米6a和红米6买哪个好 红米6与红米6a区别对比详细评测 -
 天天即时:OTA升级是什么意思
天天即时:OTA升级是什么意思 -
 环球焦点!下载App不再需要输入Apple ID的方法
环球焦点!下载App不再需要输入Apple ID的方法 -
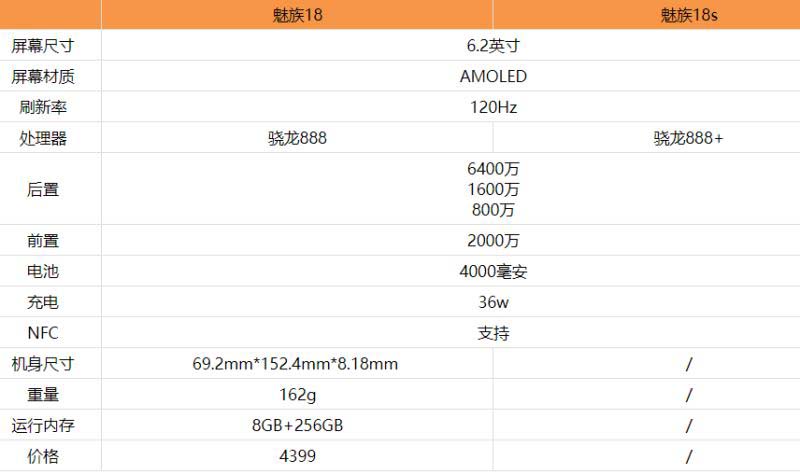 全球今亮点!魅族18s和魅族18区别是什么 魅族18s和魅族18对比评测
全球今亮点!魅族18s和魅族18区别是什么 魅族18s和魅族18对比评测 -
 天天热文:华为mate40和mate40pro哪个值得买?华为mate40对比mate40pro的区别
天天热文:华为mate40和mate40pro哪个值得买?华为mate40对比mate40pro的区别 -
 环球焦点!iPhone雷达功能怎么用?iPhone雷达功能(快播视频)查看教程
环球焦点!iPhone雷达功能怎么用?iPhone雷达功能(快播视频)查看教程 -
 环球信息:iphone手机用数据线连接电脑后只能充电无法进行文件传输的解决方法介绍
环球信息:iphone手机用数据线连接电脑后只能充电无法进行文件传输的解决方法介绍 -
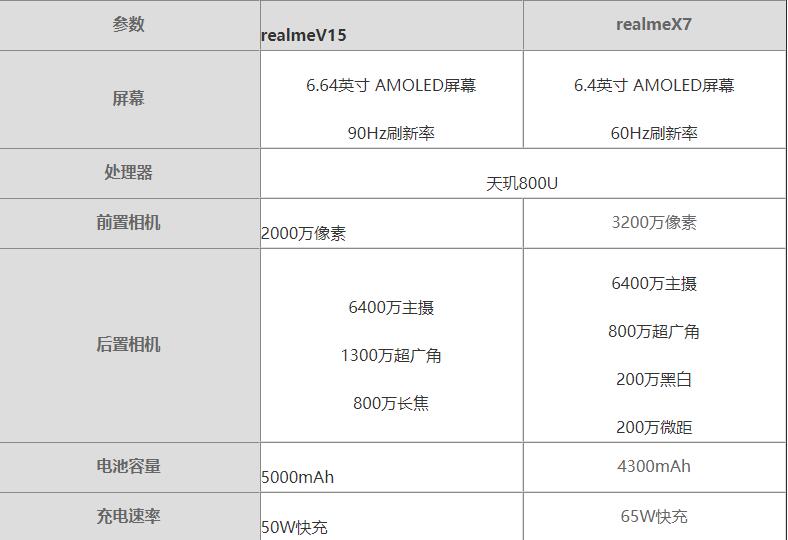 环球今热点:realmeV15对比realmeX7哪个好?realmeV15对比realmeX7评测
环球今热点:realmeV15对比realmeX7哪个好?realmeV15对比realmeX7评测 -
 当前视点!iOS 8.4 正式版发布 iOS 8.4到底升不升级?
当前视点!iOS 8.4 正式版发布 iOS 8.4到底升不升级?
精彩推荐
超前放送
- 怎样盲打及快速打字练习 用这方...
- 宝可梦探险寻宝攻略 鲤鱼王的公...
- 景点用英语应该怎么说 那你知道...
- 无锡有什么好玩的地方:每年春天...
- 快报:软科中国最好大学排名正式...
- 天天精选!伊涅斯塔 哈维的传球...
- 每日时讯!八部天龙广力菩萨 小...
- 孟加拉时间现在几点钟 孟加拉只...
- 快报:张家界凤凰旅游攻略 有信...
- 【环球速看料】窗花剪纸步骤分享...
- 当前快播:鞭炮画法简笔画 为了...
- 四色右脑记忆法靠谱吗 应该客观...
- 堆叠大陆如何制作武器 武器合成...
- 港股异动 | 天虹国际集团(0267...
- 焦点观察:AI厨师已经可以观察人...
- 世界微速讯:调理脾胃的中成药推...
- 12306火车票余票查询系统 怎么...
- 二重积分的几何意义 所以这个函...
- 一句话气死小人 对付小人的句子...
- 绿意盎然的意思 意思是百花盛开...
- 快消息!流水汩汩怎么读是什么意...
- 联通流量银行 可以通过流量银行...
- 电脑如何输入乘号 有很多方法可...
- sin75度等于多少是否带根号 用...
- 野外生存必需记住的小技巧:比任...
- 日新之谓盛德的意思是什么:这里...
- 《格列佛游记》经典佳句:国王应...
- 二本较好的医科大学有几所 全国...
- 天天新资讯:轻松掌握速记方法 ...
- 娱乐节目游戏大全 类似于不听话...
- 全球热头条丨霍氏八极拳小架的拳...
- 牛开头的四字成语拜年 我们来看...
- 惠存是什么意思 是个敬语 意思...
- 夏日绝句的诗意是什么 这首诗自...
- 成语故事大全100篇 看你一路上...
- 世界视讯!灰太狼说过的台词 让...
- 全球新消息丨鸡翅木价格多少钱一...
- 静看庭前花开花落的出处:改编自...
- 天天要闻:赛尔号谱尼真身打法攻...
- 中国哪年出现过日全食 “草莓月...
- 焦点消息!苹果“天价”发布,A...
- 国产电影记忆碎片详细剧情解析 ...
- 白酒反弹,消费板块低开高走,消...
- 电学知识 电学基础知识包括电流...
- nba季后赛规则 NBA季后赛是指7-...
- 世界今热点:苏州轻轨一号线站点...
- 环球速递!处暑拼音怎么读 告诉...
- 3A钞能力!《最终幻想》系列开发...
- qq游戏不能玩怎么办 可以检查网...
- 牛郎织女连环画简单又漂亮的画法...









