一分钟速算及十大速算技巧 秒根能在一秒钟内求出一个数的平方
哈喽小伙伴们 ,今天给大家科普一个小知识。在日常生活中我们或多或少的都会接触到十分钟速算(一分钟速算及十大速算技巧) 方面的一些说法,有的小伙伴还不是很了解,今天就给大家详细的介绍一下关于十分钟速算(一分钟速算及十大速算技巧) 的相关内容。
十分钟速算(一分钟速算和十个速算技巧)
十个手指,掌心对着自己,从左往右数。
 (资料图)
(资料图)
1.一位比十位大1 ×9。
简洁的记忆公式
一位是几个弯回几个,一个弯指左边一百位,34×9=306 89×9=801。
弯指的是把0读成十位数,弯指的是右数。78×9=702 45×9=405
2.一位比十位大9倍。
简洁的记忆公式
一位弯回几,原来的十位数是百,38×9=3.4225×9=225。
减去左边的百位数,剩下的手指是十位数,13×9=11718×9=162。
弯曲指的是分界线。向右拐一点。
3.一位等于十位×9
简洁的记忆公式
一位是几个弯回几个,一个弯指左边一百位,33×9=29788×9=792。
弯指十位数读9,弯指一位数读右。44×9=396
4.一位比十位小9。
十减一,写一百,原个位数写十,94×9 =(9-1)×100+4×10+(100-94)= 846。
用百位之差写一位(加补数),如十位加十位。83×9=(8-1)×100+ 30+17=747 62×9=(6-1)×100+2×10+(100-62)=558
添加
增减差异法
前一个加数加上后一个加数的整数,
负加数和整数之差等于和(负补数)。
+1 -2
1378+98=1378—100+2=14765768+9897=5768+10000—103 =15665
只求两个数的位置变换的两位数之和。
前面十位数加上它的个位数,乘以11等于总和。
47+74=(4+7)×11=12168+86=(6+8)×11=154
58+85=(5+8)×11=143
单眼三线加法
35427158公式
+6447859631如果不够9的话,直接用分段法加,进阶到1。
+7423344522中间数且弃掉> 19的19,前面输入1(弃掉中间的9)
17525475733,最后一位舍弃20且> 19,前面输入1(最后一位舍弃10)。
注意事项:
(1)中间数和小于9的用直接加法或分割法。
分段直线加法1+ -19 1+ -20
① 36 0427158②36 042 9158③ 36042715 9
64 178596364 178 9963 64178596 9
+74 2334452 +74 233 9452 +74233445 9
174 4547573 174 455 8573 174454758 7
②中间数有三个9:中间弃19,前面加1。
③后三个9 > 20,丢弃后20,添加之一个。
减法
大差异缩减法
公式:从被减数中减去整数,加上被减数的补数等于差。
321-98=2238135-878=7257 91321-8987=82334
-1+2 -1+122 -1+1013
(—100+2) (—1000+122) (—10000+1013)
求两个位置颠倒的两位数的差就行了。
公式:被减数的十位数减去它的一位数,乘以9,等于差。
74-47=(7-4)×9=27 83-38=(8-3)×9=4592-29=(9-2)×9=63
只要找出两个中端换位数相同的三位数的区别就行了。
公式:被减数的百位数减去它的个位数,乘以9 (9必须写在差的中间),等于差。
936—639=297 723—327=396 873—378=495
(9—6)×9=3×9=27(7—3)×9=36 (8—3)×9=45
求两个余数之差
公式:被减数减去50,其差加倍就是最终差。
73—27=(73—50)×2=46两个补数相减,用50。
63—387 = (613—500) × 2 = 226减去三个余数,用500。
812—1888 = (8112—5000) × 2 = 6224减去四个余数,用5000。
增加
十位相同,一位互补。
公式:前一个因子的十位数字加一个1和另外十位数字的乘积,再写出两位乘积,就是最终的乘积。
67×63=(6+1)×6×100+7×3=4221
387681
×32 ×74×89
216 5624 7209(不需要在十位数上加零)
法则:十位数互补,一位数相同。
公式:十位数乘以十位数加一位数,一位数乘以一位数。
76×36=(7×3+6)×100+6×6=2736562=(5×5+6)×100+6×6=3136
68×48=(6×4+8)×100+8×8=3264
一种乘法运算,其中几十位与一位互补,另外几十位与一位相同。
互补的几十位加一个1,再乘以另外几十位,然后写出两个位的乘积,就是最终的乘积。
37×66=(3+1)×6×100+6×7=2442 88888888888
46×77=(4+1) ×7×100+6×7=3542× 37
44×28=(2+1) ×4+4×8=12323288888888856
(3+1)×8=32
1的乘法运算
如果是几个高位,就输入几个,两两挨着写。加10以上先加1,写多少位?
231415
× 11
2545565
十位为一的乘法和个位数为一的乘法。
乘1位写1位,乘13位写1位,3151 61
加10位写10位,加12写10位,21加71加81。
乘十写百,乘156写百,651 36214941
用进位加进位。用进位加进位。
补充
1.被乘数和乘数有相同的十位数,个位数之和不等于10。
每个位相乘写一位,每个位相加再乘以一个十位数得到一个乘积写十位,十位相乘写一百位,进位加进位。
23 23×25=(2×2)×100+(3+5)×2×10+3×5=575
×25
57 5
2.被乘数和乘数有相同的个位数,十位数之和不等于10。
乘位写一位,加十位乘一位数得积写十位,乘十位写一百位,加进位加进位。
23 23×43=(2×4)×100+(2+4)×3×10+3×3=989
×43
989
3.被乘数和乘数的十位数之差为1,个位数之和等于10。
方法:方差公式:(A+B)(A—B)=A2—B2
52×48=(50+2)(50—2)=502—22=2496
注:①此法也可用于差为2、4、6、8、10的两个数相乘。
24×28=(26+2)(26—2)=262—22=676-4=672
②这种方法也可以推广到多位数乘法。
592×608=(600—8)(600+8)=6002—82=360000—64=359936
数字的特殊乘法
72×15=(72÷2)×(15×2)=36×30=1080 15×2→30
366×25=(366÷4) ×(25×4)=91.5×100=915025×4→100
612×35=(612÷2)×(35×2)=306×70=21420 35×2→70
214×45=(214÷2) ×(45×2)=107×90=9630 45×2→90
568×125=(568÷8) ×(125×8)=71×1000=71000 125×8→1000
38×15=(38÷2) ×(15×2)=19×30=570
48×25=(48÷4) ×(25×4)=12×100=1200
42×35=(42÷2) ×(35×2)=21×70=1470
78×45=(78÷2) ×(45×2)=39×90=3510
856×125=(856÷8) ×(125×8)=107×1000=107000
任意两位数乘以两位数的通用方法
第三步:1。单位乘法;2.将上下位数交叉相加的乘积相加;3.十位数乘法(加进位加进位)
35 34 41
×52 ×52 ×35
1820 17681435
任意三位数乘以两位数的通用方法
四个步骤:
1.把个位数上下相乘,写一位;
2.将个位数和十位数交叉相乘,将乘积相加(加进位加进位)写出十位数;
3.个位数和百位数的交叉相乘加上十位数的上下相乘,然后相加(带进位的进位)
4.将十位数和百位数交叉相乘,写到更高位。
312438
× 56 × 52
17472 22776
任意三位数乘以三位数的通用方法
五个步骤:
1.个位数相乘,写一位;
2.每个数字和十个数字相乘相加,写出十个数字;
3.把单个比特和一百个比特的叉积相加,然后乘以十个比特写出一百个比特;
4.十位数和百位数的乘积相加,写成千位数;
5.百乘百,写万。
数字越大,计算越好。
9992=998001999999992=9999999800000001
几个9数相乘;几个9数相乘;
位数减1,写成9;位数减1,写成9;
9后写8填一位;9后写8填一位;
8的前几个9,然后在8后面加几个0;几个9算几个0;
最后写个1;最后只写一个1;也就是乘法的最终产物。
99× 587 = 5864131.求补码;
99-413(补数)=586
99× 456 = 4555442.交叉减法减补数(减一次)
999-544=455
98× 897 = 8952063.补数相乘后写出(先找出两个数的每个补数,减去另一个。
98-103 = 895写在数的前面,补数相乘写在后面,哪个数不对)。
2(998的补数)×103=206
即使是小数字也算。
1062=11236 2072=42849 3072=94249
公式:百位乘百位写高位;
将百位和个位数相乘将中间放大两倍;
后面写的是个位数乘以个位数。
特殊数的除法运算
公式:
任意一个数除以15,等于它的2倍,再除以30。375 ÷ 15 = (375× 2) ÷ (15× 2) = 750 ÷ 30 = 25.
用任意一个数除以25,等于它的4倍,除以100.136÷25 =(136×4)÷(25×4)= 544÷100 = 5.44。
任意一个数除以35,等于它的2倍,除以70250÷35 =(250×2)÷(35×2)= 500÷70 = 7.142857。
将任意一个数除以45,等于它的2倍再除以90.350÷45 =(350×2)÷(45×2)= 700÷90 = 7.777。
用任意一个数除以125,等于它的8倍再除以1000105÷125 =(105×8)÷(125×8)= 840÷1000 = 0.84。
数学心算
两位数乘法
1.被乘数和乘数的十位数相同,每位数之和等于10,是两位数的乘法;
方法:(1)将乘数的一位数与被乘数的一位数相乘得到一个数。
(2)被乘数的十位数加一的和乘以乘数的十位数得到另一个数。
(3)连接两个数字就是你想要的产品。
例如:27×23 = 621 27×23 =(2+1)×2×100+7×3 = 600+21 = 621。
74×76=(7+1)×7×100+4×6=5600+24=5624
之一种和第二种方法如下:
注:如果个位数的乘积小于10,则十位数用0填充(下同)。
如31×39 =(3+1)×3×100+1×9 = 1200+9 = 1209。
两位数的1的平方,而个位数是5也可以用这个方法。
2 35×35=1225 75×75=5625 95×95=9025
这种方法也可以扩展到多个数字。
例如:498×492 =[49×{ 49+1 }]×100+2×8 = 245016。
2.被乘数的十位数和个位数相同,被乘数的十位数和个位数之和等于10的两位数相乘。
方法:①将乘数的个位数与被乘数的个位数相乘得到一个乘积;
②乘数的十位数加一的和乘以被乘数的十位数得到另一个乘积。
例如:44×28=1232 66×73=4818 33×82=2706。
3.被乘数和乘数有相同的个位数,十位数之和等于10。两位数乘法:
方法:(1)将乘数的一位数与被乘数的一位数相乘得到一个数。
(2)乘数的十位数乘以被乘数的十位数加一位数得到一个数的乘积。
例如:76×36=2736 47×67=3149 57×57=3249。
注意:①两位数的平方,如果十位数都是5,也可以用这个方法。
582=3364 58×58=(5×5+8)×100+8×8=3364
②两位数的平方,其中第十位是4,是用25减去它的一位数的补码,再乘以它自己提出的补码的乘积得到的。比如:472=(25-3)×100+32=2200+9=2209。
4.被乘数和乘数的个位数相同,十位数之和不等于10的两位数乘法。
方法:(1)将乘数的个位数与被乘数的个位数相乘得到一个乘积;
(2)将二十位数之和乘以一位数,得到乘积;
(3)将乘数的十位数与被乘数的十位数相乘,得到一个乘积:
例如:23×43=989 26×36=936
5.被乘数和乘数的十位数相同,位数之和不等于10。两位数乘法:
方法:(1)将乘数的个位数与被乘数的个位数相乘得到一个乘积。
(2)将乘数的一位数加上被乘数的一位数之和乘以被乘数的十位数,得到一个乘积;
(3)将乘数的十位数乘以被乘数的十位数,得到另一个乘积。
注:①任意两位数的平方也可用于此法。
例如:12×12=144 31×31=961 26×26=676。
6.②两位数的平方十是9。方法如下:原数减去其补数,再乘以补数乘以自身的乘积。例如:922=8464 972=9409
7.被乘数和乘数的十位数之差为1,位数之和等于10。两位数乘法:
方法:调用两方之差公式:(A+B)(A—B)=A2—B2。
比如52×48=2496,分解成(50+2)(50—2)=502—22=2496。
注:①这种方法也可用于差为2、4、6、8、10的两个数相乘:
24×28=(26-2)×(26+2)=262-22=676-4=672
②这种方法也可以推广到多位数乘法:
592×608=(600-8)(600+8)=6002—82=359936
8.任意两位数的乘积:
方法:(1)被乘数的十位数乘以乘数的个位数的积和被乘数的十位数乘以乘数的个位数的积之和给出一个数(即叉积加10)。
(2)两位数相乘得到一个数,二十位数相乘得到一个数× 100。
(3)三位数之和就是你所求之积。
例如:24×35=22+620=840
24×35=(2×5+3×4)×10+2×3×100+4×5=220+600+20=840
以上方法均可应用于十进制乘法,通过“计数定位法”根据计算结果确定小数点的位置(多位数乘法也是如此)。
多位数乘法
1.操作中涉及的问题:
1.什么是补语?
十、百、千、万的数称为补数。也就是说,两个数之和等于10,100,1000,10000...它们是相辅相成的。
2.求补数的方法:之一位是九,最后一位是十。
3.补码的特点:几位数是一个数,补码必须是几位数。例如:
98的补码是02,9985的补码是0015,以此类推。
4.补数乘法的定位:乘数是多少位,被乘数右移几位就是乘积的单位。
2.计算方法:
1.112=121,1112=12321,11112 = 1234321等等。
如果不是用11连接,可以用11连接,分两步计算。
比如2222×5555 = 1111×2×1111×5 = 1234321×10 = 12343210。
2.任意一个数乘以11,前两位和后两位保持不变。中间的数字是两个相邻数字的和:
例如:63×111=6993
3.如果被乘数用99(不管多少位)连接,就从被乘数的之一位减去被乘数的补数,差后再加上补数。比如:
(1)99999×99999 = 99980001(99999的补码是0001)
(2)999×65 = 96435(65的补数是35,999—35 = 964)
(3)99999×726485 = 726484273515(726485的补数是273515)
(999999—273515=726484)
4.如果被乘数满足前4个和后5个且中间数用大数连接,
方法如下:前四位减一半,后五位加一半,中间位9,如果中间位不足9,补数在低位加0,最后扩大10倍。比如:4995×758 = 3786210(785的补数是242,一半是121)
5.两个乘数都接近于成百上千的乘数...:
1.两个乘数都小于百、千和万...计算方法:
一个乘数减去另一个乘数的补数(接近100个数乘以1,接近200个数乘以2……)。
在得到的数上加一些零(接近几百个零,几千个零,三个零…)。
加上两个数的补数的乘积。
例:1,987×986 = 973182(987的补码是013,986的补码是014)
987—014=973000+182=973182
987×986=(987—014)×1000+013×014=973000+182=973182
2.1968×1972=3880896
1968×1972 =(1968-28)×2×1000+32×28÷= 3880000+896 = 3880896(1968年的补数是32,1972年的补数是28)
2.这两个数字都大于数百、数千……
该方法:
(1)将一个乘数的分数与另一个乘数相加(接近100乘以1,接近200乘以2……)
(2)在得到的数后面加几个零(第1部分)
(3)加上两个数的分数乘积。
例如:1,112×105 = 11760 112×105 =(105+12)×1×100+12×5 = 11700+60 = 11760
2.204× 215 = 43860 204× 215 = (204+15 )× 2× 100+4× 15 = 43800+60 = 43860
3.一个乘数大于百、千、万,另一个乘数小于百、千、万。
该方法:
(1)先将较大数的分数加到较小数上,(接近100的数乘以1,接近200的数乘以2 …)
(2)在得到的数字后填入一些零(接近百的数字两个零,接近千的数字三个零……)
(3)最后,减去较大数的分数和较小数的补数的乘积。
例:①256236(489的补数是11)
524×489=(489×24)×5×100-24×11=256500-264=256236
②1015×998=1012970
1015×998=(998+15)×100—15×2=1013000-30=1012970
不及物动词任意多位数的乘法:(按大中组计算)
1、2、3是小数组,4、5、5是中数组,7、8、9是大数组(一般使用位数较少的被乘数)。
(1)当被乘数满足1、2、3时,方法是:
1:低位补码减一次(或加倍)。
被乘数是2:较低的负补数的两倍(或两倍)。
3:减去低位补码三次(或三次)。
(2)当被乘数的每一位遇到4、5、6时,方法是:
是:标准减半补,下加一次补。
乘数是5:标准减补数的一半。
是:标准减一半的补,低的减一次。
(3)当被乘数的位数满足7、8、9时,方法是:
是:基本补码减一次,低位补码加一次。
被乘数是8:基本补数减一次,低位补数加两次。
是:基本补码减一次,低位补码加三次。
(4)当被乘数遇到989697等大数的运算时,方法如下:
被乘数的后位补10,前位固定9,当前位满足6、7、8时,补9次(所有次都是低位补),最后被乘数的之一位减一次。
注意:如果被乘数的之一位不是大数,则之一位为1,低位减去补数两次;之一个数是2,较低的数减补三次;之一名是3,标准减去补数是一半;低位补加一次,之一个是4,标准补减一半;之一名是5,标准减一半,下级减一次。
注:五倍(或五倍)的低位补数等于标准补数的一半。几十倍(或10倍)的下补码等于一倍的标准补码。
破碎公式
加一个。负一。五加五。
1、2、3依次递减,4、5、6减半,7、8、9视为10,加除法,减乘法,全零不算。
多位数除法
1.速度算法
除法的目的是求商。但是,当你突然看不出被除数中包含了多少个商时,可以用试商和估商的方法。如果被乘数的更高位数含有几个约数(即几倍的商),可以从标准数开始加几倍的补数,得到的数就是商。
2.计算和定位:
除数是一位,一位是标准,除数是两位,十位是标准,除数是三位,百位是标准,以此类推。
3.小型阵列:
1次:标准数加一次。
被除数含商2倍:从标准数加补数2倍。
3次:从标准加补码开始的三次。
4.中数组:当除数包含4、5或6倍除数时,方法为:
4次:前面位置加一半的补码,减去标准补码的一次。
被除数包含5倍商:之一位加一半补数,标不动。
6次:之一位加半个补码,标准加一次补码。
5.大型阵列:
9次:之一位补一次,标准位减一次。
被除数含商8次:之一位数补一次,基本位数减两次。
7次:之一位补一次,标准位减三次。
几何证明问题的公式
证明几何题并不难。之一,通过考试;
认真研究每一个字,把命题看几遍;
看图,正确思考。如果你知道,你应该写所有的证明。
除了知识更重要,证明方法要优化;
紧扣题意,分析难点,根据结论找条件;
字迹工整清晰,论证步骤写得很好。
一些数的和
1.自然数之和:1+2+3 …+n = 1/2n (n+1)
2.奇数和:1+3+5+…+(2n-1) = N2
3.偶数和:2+4+6+…+2n = n (n+1)
实用性知识
1.快速计算土地亩数(单位:米)
宽度加宽一半,底和乘以长边。
往前移三位,土地亩面积就好算了。
注:如果是三角形、梯形等图形,可以这样计算。
半个区域加上区域,向前移动三个站点。
2.给猪称重
胸围(cm) 2×体长(cm) ÷7600=猪体重(kg)
3.测量牛或羊的重量:
胸围(cm) 2×体长(cm) ÷5400=体重(kg)
四。1-14岁正常人的身长体重:
体长(厘米)=(年龄× 5)+80
体重(公斤)=(年龄× 4 )×+16
数学游戏
1.猜年龄和出生月份:(出生月份×2+5)×50+年龄-365。
2.猜猜男女人数:(总人数×2+5)×50+女生人数-365
3.猜房子的数量:(房子总数×2+7)×5+大房子数量-20。
4.猜一下排位:(姐妹总数×2+3)×5+排位。
运用
1.两位数乘法:
63×67= 42×48= 88×64= 66×37= 21×23=
42×43= 24×84= 32×27= 54×38=
2.多位数乘法:
113×108= 998×985=
9999×4268= 1012×997=
有趣的算术
速效药方
简洁的记忆公式
加一个。负一。五加五。成对的线。真是绝配。
秒根:能在一秒钟内求出一个数的平方。
平方:一个数自升的乘积。
速效药方:能在一秒钟内快速有效地根出一个数值的药方。
1、增加一种根部开口的计算方法。
添加原因:
每当这个数大于正整数时,之一个数字加上最后一个数字的一位数之和就是这个数的开根。
例如:√121 = 11 10×10 = 100√441 = 21 20×20 = 400√961 = 31 30×30 = 361 20-1 = 19。
\- 全球热推荐:btm论坛(bt论坛下载)
- 家居巨头宜家引入AI功能:下次沙发设计交给AI 天天快资讯
- OpenSSL 1.1.1将于2023年9月停止支持 官方要求用户升级-环球今日讯
- 映众中低端40系隐藏电源线
- 《SOULVARS》推出Steam体验版 主机版紧张筹备中
- 天天热头条丨红外监控摄像机(红外监控摄像头)
- 性能巨牛!惠普战X 2023 锐龙版笔记本电脑只要5499!
- 全球观热点:安盛天平车保险怎么样?(安盛天平保险怎么样 天平车险理赔速度快不快)
- 百亿补贴专享!联想小新Pro 14到手仅4260元
- 环球焦点!谷歌计划为高端ChomeOS笔记本推出Chromebook X品牌
- 专家称刷题应试正在被淘汰:只顾机械刷题恐怕很难考上大学
- Redmi Note 12R现身电信终端产品库:5000mAh电池加持|全球热点评
- 全球热门:西行漫记:喀什售后走一遭
- 性能释放拉满!华硕天选4 Plus特价8499元!-精选
- 消费者不傻!iPhone 14 Plus成最不受欢迎产品_天天新视野
- iOS 17的屏幕距离功能 安卓为何没有
- 环球最资讯丨游戏玩家不要错过!机械革命蛟龙16S暴跌至6499元
- 一加Ace 2 Pro更多规格曝光:配备静音滑块,支持红外遥控
- 山东女篮主力 16岁小将张子宇身高2米27已超姚明 环球新视野
- 邓铁涛62个经验方(邓铁涛治静脉曲张方) 全球热点
- 环球动态:实测RTX4050对比4060性能提升多少?哪些机型值得买
- 烛之武退秦师词类活用特殊句式(烛之武退秦师词类活用)
- 极限路书之西行漫记:与70迈A810一起行摄英雄之路 挑战12000公里新疆环游|全球百事通
- 天天微动态丨瑞典哥德堡大学试验鱼菜共生农场 - 由鱼粪提供动力
- 苹果公司的机器学习负责人离职 将运营AI智囊_世界讯息
- 续航时间很顶!ThinkBook 14p 到手仅需3999! 全球视点
- 联想RTX 4060游戏本只要5699元 实测3A大作后简直是性价比之王
- 锐龙9 7940HS强势登场 雷蛇灵刃14锐龙版评测
- 《2077》版本更新1.63推出 含各种游戏性和任务修正-全球观热点
- 全球动态:影院回应屏摄电影被怒斥:对胶片有损伤 网友质疑:侮辱智商?
- 粉色和什么颜色最配墙壁(粉色和什么颜色最配)
- 当前热门:小鸡宝宝考考你高血压可能影响视力,这种说法
- 像素版《战地》在线人数超6万 是《战地2042》的6倍 环球热点
- 微软/动视暴雪的合并引起新西兰监管机构对云游戏的关注
- 两战全胜!国足2-0击败巴勒斯坦 武磊、蒋光太破门
- 苦咖能减肥吗(苦咖易瘦法)
- 世界即时:不成语大全四个字(不成语)
- 《别叫我赌神》发“骄阳”主题大片 发哥容光焕发
- 新西兰对微软收购案表示担忧:决定日期延至7月17日
- cx 330是什么意思(cx330是什么意思?)|新动态
- 当前速递!国产显卡第一次!摩尔线程发布DX11社区版驱动 能玩5款游戏
- 世界最大邮轮“海洋标志号”首次出海试航:比我国魔都号大一倍 天天时快讯
- 当前热文:中职中专什么意思(ldquo 中职 rdquo 什么意思)
- 全球视讯!到2025年 印度可能向全球出货将近五分之一的iPhone手机
- 快播怎么看3d电影具体操作图解(快播怎么看a片) 热消息
- 新能源坦克500将上市:预售36万 可挂绿牌
- 快看点丨米哈游获全国版权示范单位称号:版权领域最高荣誉!
- 金庸群侠传3无敌版之武林至尊下载(金庸群侠传3无敌版之武林至尊)
- 网友希望迪士尼暴雨天退票 官方回应:售出不退 可游玩室内项目
- 格力发布618战报:销售额90亿 不足“老对手”小米的一半 全球观点
- 手机易拆卸电池或回归 近六成网友:深恶痛绝-全球微资讯
- 版本号踏入“三位数”:Opera浏览器推出100版本正式更新
- 环球关注:一加首款折叠屏手机外观首曝:直角中框、后置哈苏三摄
- 太空漫游!《星空》限量版XBOX手柄/耳机开箱图赏|每日热讯
- 日电信业务法生效 保护用户不被违规分享Cookie
- 《幻塔》宣布8月8日登陆PS平台 典藏版售价798港币
- 推特首位AI Coser将突破40万粉!图片人气超高|世界观焦点
- 雷军参加武汉大学2023毕业典礼、称有句话让他受益终身
- 世界热文:云米和小米是一个品牌么(云米和小米是一家吗)
- 当前信息:谁说没有性价比 价格下来后的4070游戏本真香
- 试玩版上线 免费PvP动作游戏《Warhaven》支持中文
- 酷派手机怎么样好用吗((coolpad)酷派手机怎么样)
- 环球速递!索尼玩家奇葩请愿:要求《星空》成PS5独占
- 狂野之心推出全新凶恶彼岸飞更新内容|每日速读
- 【当前独家】学生帽穗丢了老师无实物拨穗 网友:考验的是演技
- 张兰直播近6小时带货超525万 网友:她的快乐都藏不住了
- 采用模块化可拆卸设计:Fairphone 5手机承诺提供5年保修
- 毕业典礼上学生帽穗丢了:老师无实物拨穗-今日看点
- 技嘉将发布UD-A620I-X主板 价格预计千元以内
- 环球快资讯:《原神》推出犬坂吠吠小夜灯充电宝套装 到手269元
- 函授教育是什么意思啊(什么是函授教育)_环球视讯
- 全球微头条丨索尼电视将支持Zoom视频通话 仅限特定型号
- 前沿热点:空气密度是多少立方厘米(空气密度是多少?)
- ROG掌机官方游戏画面设置:更流畅体验3A大作!
- 雷军现身武大毕业典礼 雷军2023武汉大学演讲内容全文|最新资讯
- 百花齐放的江湖门派,为何在武侠游戏里“哑火”了?
- midjourney卡通提示词怎么写?midjourney卡通风格关键词案例分享
- 【天天播资讯】网易有道云笔记免费用户最多登2台设备 升级VIP可解锁限制
- 高校回应宿舍热水费5275元 外包给公司管理
- 当前报道:百家云发布AIGC新品「市场易」大模型
- 张兰直播近6小时带货超525万 直播间还播放《好日子》-天天热资讯
- 《FF7RE》制作人:公司很多人让我们做《FF6RE》_世界信息
- 华为nova6啥时候上市(华为手机nova6上市时间)
- 【环球速看料】信用卡停息挂账的条件有哪些?信用卡能不能办理停息挂账
- 华为回应向日本中小企业收专利费:合理收费是创新的结果而非目的
- 【世界报资讯】中小企业贷款行业发展趋势及市场现状分析
- 中国地震台网正式测定-全球新要闻
- 天天视点!文旅部:全面推进“一厕一码”在线评价反馈平台建设
- 微头条丨2023年养老金的涨幅3.8%,工龄20年、30年、40年各能涨多少?计算方法来了
- 哪吒汽车CEO谈国内新势力竞争:仿若小朋友掐架
- 日版黑暗荣耀?网飞悬疑剧《火烧御手洗家》正式预告-世界今热点
- 苹果投资2亿美元助力全球种族平等正义计划|全球快播
- 囊括全欧亚大陆!逆水寒手游公布未来10年开发计划
- 华曙高科(688433):设备为基 多元发展 争做国际一流工业3D打印厂商|世界聚焦
- B站618,有人开播4天GMV提前破亿!_焦点速看
- 为何“网络大V”对河北联通全屋光宽带赞不绝口?听听大V主播们怎么说!
- 柔顺对头发的伤害大吗(柔顺)
- 《星空》游戏本地化问题迭出 玩家请愿增加语言支持|天天微头条
- 研究发现长期服用低剂量阿司匹林可能增加健康老年人的贫血风险 当前关注
- 每日快播:“双星”合璧,星纪魅族集团与极星成立合资公司
新闻排行
-
 关注:iCloud Drive是什么以及iCloud Drive是什么意思?
关注:iCloud Drive是什么以及iCloud Drive是什么意思? -
 【播资讯】红米6a和红米6买哪个好 红米6与红米6a区别对比详细评测
【播资讯】红米6a和红米6买哪个好 红米6与红米6a区别对比详细评测 -
 天天即时:OTA升级是什么意思
天天即时:OTA升级是什么意思 -
 环球焦点!下载App不再需要输入Apple ID的方法
环球焦点!下载App不再需要输入Apple ID的方法 -
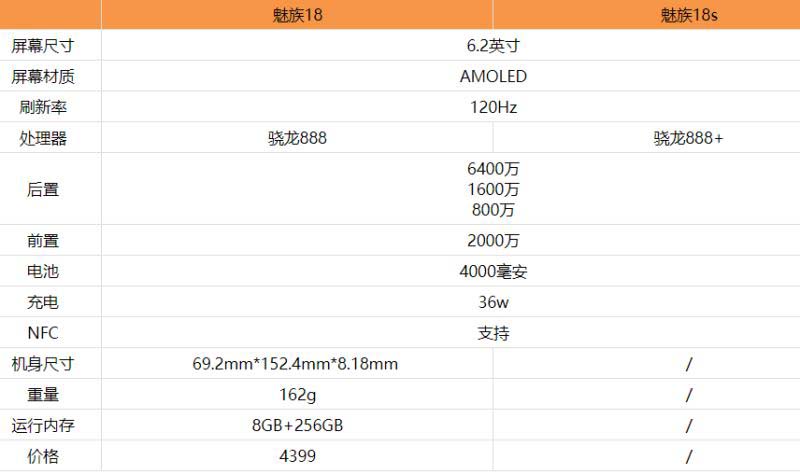 全球今亮点!魅族18s和魅族18区别是什么 魅族18s和魅族18对比评测
全球今亮点!魅族18s和魅族18区别是什么 魅族18s和魅族18对比评测 -
 天天热文:华为mate40和mate40pro哪个值得买?华为mate40对比mate40pro的区别
天天热文:华为mate40和mate40pro哪个值得买?华为mate40对比mate40pro的区别 -
 环球焦点!iPhone雷达功能怎么用?iPhone雷达功能(快播视频)查看教程
环球焦点!iPhone雷达功能怎么用?iPhone雷达功能(快播视频)查看教程 -
 环球信息:iphone手机用数据线连接电脑后只能充电无法进行文件传输的解决方法介绍
环球信息:iphone手机用数据线连接电脑后只能充电无法进行文件传输的解决方法介绍 -
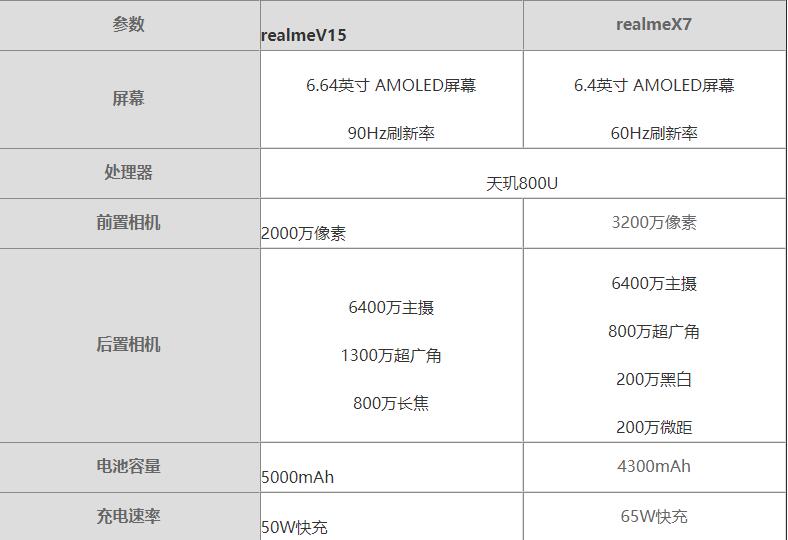 环球今热点:realmeV15对比realmeX7哪个好?realmeV15对比realmeX7评测
环球今热点:realmeV15对比realmeX7哪个好?realmeV15对比realmeX7评测 -
 当前视点!iOS 8.4 正式版发布 iOS 8.4到底升不升级?
当前视点!iOS 8.4 正式版发布 iOS 8.4到底升不升级?
精彩推荐
超前放送
- 深圳地铁表白专列 深圳将用地铁...
- 一分钟速算及十大速算技巧 秒根...
- 宫锁珠帘舒畅牡丹云嫔是谁扮演的...
- 七十六个经典国学常识汇总:十大...
- 全球热议:海淘推荐 小编整理了...
- 埃及魔法膏真假鉴别 在埃及买买...
- 先驱者腿甲哪里掉 在魔兽世界这...
- 手写板万能驱动下载 告诉你具体...
- 江宁谷里薰衣草庄园门票 在这里...
- 全球速读:单杠怎么练胸肌最好(...
- 家庭装什么宽带最划算 用电信猫...
- 男生发型名称大全 每个男生都剪...
- 解析智能手机会变慢的真正原因 ...
- 史上最详细的surface pro评测:...
- 商业地产广告语 我们来关注一下...
- 全球最资讯丨一般根雕值多少钱为...
- 职称英语讲解 职称英语考试有哪...
- 如何使用电脑?使用电脑正确方法...
- 【全球快播报】白玉雕刻一级和田...
- 倒立训狗 泰迪犬一般教多久就知...
- 酒喝干再斟满是什么歌 这首歌是...
- 盗梦空间这几个细节你看懂了吗 ...
- 环球观察:新商业文明的四个准则...
- 怎么更改appleID?苹果手机的id...
- 好看的宝宝毛衣 看着这些好看的...
- 【天天新视野】无法获取网络地址...
- 科目三考试详细步骤流程分享 需...
- 叫做和叫作的区别是什么(叫做和...
- 梦幻西游百无禁忌符石 梦幻西游...
- 打开cda文件的技巧 小编将向您...
- 怎么看电脑是x86还是x64?window...
- 看热讯:孙艺珍婚后买入244亿韩...
- 冬奥会手抄报简单又好看:可以给...
- 中国瘦人增肥网 增肥方法和增肥...
- 天天快看点丨在松江老街老宅的展...
- 劲的部首和拼音解释 以下文章是...
- 3大类12种液压阀工作原理 电磁...
- Win10怎么清理Hosts文件?怎么清...
- 宝宝成长日记范文大全 不得不感...
- 天涯影视网的热帖盘点 哪一部影...
- 天天热议:完整的孙子兵法全文翻...
- 天天消息!用木鱼石杯子有危害吗...
- 马钱子炮制解毒方法 中医常用马...
- 洛克王国独角兽怎么进化 可以让...
- WiBox播放器的简单使用过程 网...
- 这5个Excel小技巧也要学 教你怎...
- 【世界快播报】崩组词是什么有哪...
- 世界热讯:赫赫伟绩的成语解释及...
- 1999元!锐龙7000! 这款迷你主...
- 天天速看:盘点十部最经典的古装...