当前资讯!罗素悖论及其他 辛普森悖论是数据分析中最常见的悖论之一
最近这段时间总有小伙伴问小编罗素悖论(罗素悖论内容) 是什么,小编为此在网上搜寻了一些有关于罗素悖论(罗素悖论内容) 的知识送给大家,希望能解答各位小伙伴的疑惑。
 (资料图片仅供参考)
(资料图片仅供参考)
罗素悖论(罗素悖论的内容)
和数据打交道越多,就越有可能对数据产生绝对的信任感。但事实上,在实际业务中,数据往往会“说谎”。今天,我将向你介绍数据分析中的三个常见悖论:
1.辛普森悖论
辛普森悖论是数据分析中最常见的悖论之一。举个最实际的例子:
雅宝某学期期末考试,有数学、物理、化学三科。a的数学比B高2分,物理比B高15分,化学比C高3分。A的总分比B的高吗?
很多人会说,这不是废话吗?问题太简单了。当然A的总分比B高!
其实很可能A的总分比B低。不要惊讶。我们不妨看看另一个例子:
许多人喜欢看NBA比赛。近年来,詹姆斯和库里都给球迷留下了深刻的印象。有勇有谋,詹姆斯和库里的两分和三分投篮命中率如下表所示:
其中包括:
两点命中率=两点命中/两点投篮* 100%
三分球命中率=三分球命中次数/三分球出手次数* 100%
那么,这场比赛詹姆斯的投篮命中率比库里低吗?
投篮命中率=(两分球+三分球)/(两分球+三分球)* 100%
很多人也会说,这不就和上面期末考试的题一样简单吗?不言而喻,詹姆斯的投篮命中率肯定比库里低!当我们拿出详细的数据时,它看起来真的是这样的:
但这真的是废话吗?再来看看这两兄弟在另一场比赛中的表现:
这场比赛,詹姆斯和库里,谁的投篮命中率高?如果这次你还说这是废话,当然库里投篮命中率高,那你这次就没那么幸运了。我们来看看详细的数据:
是的,你没有看错。詹姆斯的两分命中率比库里低,三分命中率比库里低,但综上,詹姆斯的命中率比库里高!
问题来了。这是怎么回事?这不符合常识!
这种“非理性”的现象在数据分析领域时不时会遇到,业内有一个专门的术语:辛普森悖论。
具体来说,在进行小组研究时,有时在每个小组比较中占优势的一方有时在总体评价中是失败的一方的“悖论”现象,称为辛普森悖论。
现实中的许多数据,通过辛普森悖论,显示出导致错误的结论。比如现实中,多做多错,少做少错,不做就是好的。
一个经常犯错的人,并不能证明他就不如犯错少的人。可能是他花更多的时间在更复杂更容易出错的工作上。
2.罗素悖论
罗素悖论属于数理统计中永远无法回避的悖论。这个悖论简单、美丽、奇特,甚至引出了第三次数学危机的解决。
罗素悖论的准确表述应该是:
如果有一个 *** 由所有不属于自身的 *** 组成,即A = {x | x x},那么A包含在A中是否成立?如果为真,则不符合项X不属于A;而如果A不包含在A中,那么X不属于A。
罗素怕很多人理解不了这个悖论,所以给出了一个通俗的版本:
假设一个城市的人都是理发师给他们理发,理发师突然说:“我只给这个城市不自己刮胡子的人刮胡子!”然后,别人对理发师说:那你自己刮胡子吗?
如果他自己不刮,那么他就属于“不刮自己的人”,按照他的说法,他会自己刮;如果他自己刮胡子,就属于“自己刮胡子的人”。据他说,他不应该自己刮胡子。
3.伯克森悖论
当不同组的数据合并后,每个组原有的一些规律就会消失。当这种情况发生时,合并后呈现的新法律甚至可能与各个群体原有的法律相违背。
比如某一种治疗方法,在不同的组里对患者的身体恢复是有害的,但是当我们把所有组的数据放在一起看,就会发现其实对患者的身体恢复是有帮助的。
怎么发生的?
当各组的构成差异较大时,可能会出现上述现象。
比如,如果选择了患者数量,以至于两组试验的患者构成差异很大(老人、儿童、成人的比例差异很大),简单地将数据结合起来,就会得出有害治疗变成有益治疗的结论。
假设有一个双盲试验(受试者和研究者都不知道哪些受试者属于对照组,哪些属于实验组)。患者分为两组,每组120人,但两组患者年龄结构差异较大(之一组分为10、20、30、60人,第二组分为60、30、20、10人)之一组患者会接受治疗,第二组患者不接受治疗。
总的来说,结果表明治疗对患者是有益的,接受治疗的患者的恢复率高于未接受治疗的患者。
但是,当你深入研究两组中的每一个患者群体时,你会发现,在所有的患者群体中,没有接受治疗的患者痊愈率是上升的。
我们注意到每组中不同年龄的患者数量不同,甚至差异很大,这就是为什么我们得到了错误的结果。在这种情况下,如果简单地把两组数据结合起来,很容易得出错误的结论。
\- 【快播报】工厂防暑降温措施 方式主要分为自然降温和利用设备降温
- 苹果12推迟发布:如何在不吊消费者胃口的情况下实现利益更大化?
- sam辅助功能教程(sam解锁教程)
- 世界热点!金鸡独立打一个生肖 谜底生肖是龙 因为龙拳招式显飘逸灵动
- 章鱼血液的颜色是什么 本文将详细的介绍这个问题的答案_独家
- 全球通讯!一加仑等于几升 英制的一加仑等于精确值下的4.546 092升
- 火影忍者羁绊6.92攻略 火影忍者束缚各种装备的策略来了
- 仿写彩色的梦第二三段 拟人和丰富的想象力使句子更加生动形象
- 工业自动化产品有哪些 工业电气自动化产品如何写类别词 天天关注
- 个性网名大全正式上线 小编要安利快乐幽默的个性昵称
- 【手慢无】618入手超值!ThinkBook 16+酷睿版5199元带走
- 全球观速讯丨知了还在叫着夏天是什么歌 是电视剧《穿越夏天》的片尾曲吗
- iOS 17升级方法看这 所有人都能升
- 去眼袋的四种经典手术方法 内切开术适合皮肤比较紧绷的年轻人_今日讯
- 天天热讯:办公软件操作技巧 教你怎么操作Word自动显示修改后的位置
- 剑网3华清宫攻略大全 来说说我们慢慢摸索出来的方法
- 世界热文:dnf创作者需要技术吗 创作者是不是玩家最喜欢的职业之一
- 了解秦国战将白起的一生 其熟悉兵法善于用兵 辅佐秦昭王屡立战功
- 快看:鲁迅的第一篇现代版白话小说 今天小编就带你重读《狂人日记》
- 怎么大规模鉴定miRNA靶基因?miRNA靶基因鉴定的首选工具介绍|精彩看点
- 速递!我想画个什么样的太阳送给谁 以下是小编对这个问题的总结
- 钢琴好学吗 如果到了合适的年龄 自学钢琴也不是特别难
- 看完大模型们作答的高考作文,对AI的鼓吹与恐惧皆可缓一缓了
- 焦点速讯:坎儿井的水源 坎儿井主要由竖井、地下涵洞还有什么组成
- 世界看点:爱护眼睛的顺口溜:连续阅读有时间限制,还要经常练习护眼三操
- 快资讯:分析师为苹果普及Vision Pro献策:收购迪士尼
- 【手慢无】钜惠超低价!机械革命无界14+跌破4000
- 【手慢无】合金钢材 极川铝合金笔记本支架秒杀价69元-今日热文
- 洛克王国炽红莲兽技能 红莲兽就是走物质攻击和速度之流的吗|世界观速讯
- csgo开哪个箱子比较值的推荐?csgo倒卖箱子挣钱吗?
- csgo开箱网站绑定steam?csgo手机开箱软件叫什么?
- csgo怎么一次性开100个箱子?csgo新手前20个箱子必出吗?
- 世界环境日:“减塑捡塑” 让环境更美好
- csgo国际服开箱子国服能用吗?csgo开箱技巧看完你知道了吗?
- Failed to connect to zw.gozuowen.com port 80: Timed out
- 京东百亿补贴!ROG 4060游戏本到手价8999元|天天讯息
- csgo一周掉几个箱子?csgo满级了是不是不掉箱子了?
- 天天快报!比尔·盖茨:现在称我为游戏玩家可能没错
- 百思图男鞋子价格(百思图男鞋) 要闻速递
- csgo开箱积分赛怎么参加?csgo打竞技掉箱子吗?
- Win11发布预览版更新:新版文件管理器绝了
- 环球快播:【手慢无】性能突出!戴尔游匣G15游戏笔记本低至4699元
- 热点!曝《P3RE》十一月发售 定名为《Persona 3 Reload》
- 【手慢无】新品发售尝鲜价!惠普战99创作本低至5699元|全球信息
- 苏州到杭州多少公里路_苏州到杭州多少公里_环球即时看
- 天天新动态:员工罚款收入会计分录_扣员工罚款会计分录
- 有关西藏的电影有几部_有关西藏的电影
- CSGO开箱网站还有哪些?csgo买箱子和钥匙去哪个平台?
- csgo怎么开箱子不显示新物品?csgo新手前20个箱子必出吗?
- 宁波电视台讲大道重播_宁波电视台讲大道 全球热头条
- 王心凌歌曲爱你舞蹈视频_王心凌歌曲-天天关注
- 丁小猫的结局_丁小猫_快资讯
- 女杀手用脚闷死人_女杀手
- 环球信息:数字电子技术(数字电子)
- 每日时讯!外媒称《暗黑4》皮肤太贵 换算购买力后比《上古卷轴:湮灭》高出一倍
- 新世代生存射击手游《超凡先锋》今日上线 邀你畅爽开金! 天天新要闻
- 世界今日报丨世界五大宫殿分别是什么国的宫(世界五大宫殿)
- 世界报道:2023年下半年河南南阳自考时间安排
- 短讯!【手慢无】性价比无敌!机械革命无界14只要3899元
- 【手慢无】618值得冲!华硕无畏Pro15只要4998元
- 国网六安市叶集供电公司 安徽省首个35千伏变电站荣获“中国电力中小型优质工程奖”|焦点速讯
- 新资讯:“访万企,读中国”上经贸大2023年社会调查项目启动
- 当前播报:中国与突尼斯签订联合考古协议
- 【手慢无】618购物狂欢 机械革命无界14+锐龙版跌至3999元_当前报道
- 消费者商家“算法”不一 “小份菜”推广难
- 首都机场安保公司扎实开展“安全生产月”主题教育工作
- 端午假期出行机票价格更便宜 热门航线仍有折扣-全球消息
- 【新要闻】【手慢无】618特惠 ROG魔霸7 Plus游戏本超值热销价格低至8999元
- 中国十七冶集团房屋分公司总会计师徐庆勇到当涂南部新城项目开展“送清凉”慰问活动
- 看点:【手慢无】满血4060+13代酷睿 神舟战神游戏本5898元
- 全球看点:“迈向全面复苏”为主题 香港国际旅游展将举行
- 每日时讯!msvcr100.dll怎么删除(msvcr100 dll是什么)
- 支付宝怎么查询高考成绩?支付宝查高考成绩怎么查?|世界播报
- 每日讯息!ICT中国·高层论坛|移动物联网高质量发展论坛在京举办
- vivo X100/Pro/Pro+什么时候发布 发布时间日期曝光 环球观天下
- 今日热闻!AMD Zen5 架构处理器数据疑似曝光, 锐龙 8000 系列要来了?
- 环球观点:华为发布100%自主数据库:数据安全有保障了
- 周鸿祎演示360智脑写高考作文 冯仑:及格 但不打动人_即时焦点
- AMD 锐龙 8000处理器 正式确认: IPC增幅高达19%!
- 每日快看:掉线全责!《暗黑4》全球首位满级硬核角色死亡
- 高考加油!大学生考点摆摊卖9.85与21.1元花束 世界观热点
- 当前快看:caj文件怎么转换成pdf格式(caj转换成pdf网页版)
- 环球即时看!AMD Zen4c 霄龙细节曝光:升级4nm,128核心256线程碾压一切!
- 海泰发展(600082):MACD指标DIF线上穿0轴-技术指标上后市看多(06-08)|天天报道
- 即时看!DeepMind 的人工智能系统 AlphaDev 发现的排序算法可能彻底改变计算基础
- 每日观点:相当炸裂的苹果头显,直接炸飞苹果市值6000亿
- 谷歌DeepMind打破十年算法封印,AlphaDev惊世登场,颠覆人类算法格局!
- 婚车遇上高考车队:新郎下车发喜糖 互送祝福_全球今日讯
- 曝小米MIX Fold3配备潜望长焦:看齐13 Ultra 全球快看
- 【手慢无】618年中大促!联想小新Pro16最低只要5489元-世界视点
- 国企总经理与女子牵手逛街被免职 接受纪委核查
- “一到高考就下雨” 这究竟是巧合还是气候使然_全球热点
- 天津与中国邮政集团签署全面战略合作协议 在金融、快递等领域深度合作
- 全球唯一魔戒万智牌即将发售 公司发布百万美元悬赏 世界即时
- 精准打击快打快撤 直击车载榴弹炮战术考核 天天快播报
- 238 层 4D NAND 闪存量产,国产手机或率先使用,传输速度每秒 2.4Gb-每日视点
- 今日看点:邮寄携带粽子 出入境须谨慎
- 吕蒙正的妻子究竟是谁(吕蒙正的故事)
- 考生如何缓解压力?心理专家送上锦囊
- 每日快报!苹果头显成本只有43%?
新闻排行
-
 关注:iCloud Drive是什么以及iCloud Drive是什么意思?
关注:iCloud Drive是什么以及iCloud Drive是什么意思? -
 【播资讯】红米6a和红米6买哪个好 红米6与红米6a区别对比详细评测
【播资讯】红米6a和红米6买哪个好 红米6与红米6a区别对比详细评测 -
 天天即时:OTA升级是什么意思
天天即时:OTA升级是什么意思 -
 环球焦点!下载App不再需要输入Apple ID的方法
环球焦点!下载App不再需要输入Apple ID的方法 -
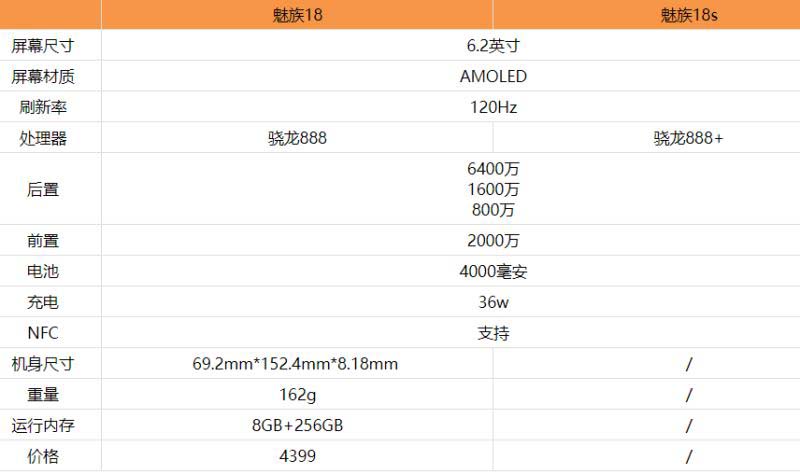 全球今亮点!魅族18s和魅族18区别是什么 魅族18s和魅族18对比评测
全球今亮点!魅族18s和魅族18区别是什么 魅族18s和魅族18对比评测 -
 天天热文:华为mate40和mate40pro哪个值得买?华为mate40对比mate40pro的区别
天天热文:华为mate40和mate40pro哪个值得买?华为mate40对比mate40pro的区别 -
 环球焦点!iPhone雷达功能怎么用?iPhone雷达功能(快播视频)查看教程
环球焦点!iPhone雷达功能怎么用?iPhone雷达功能(快播视频)查看教程 -
 环球信息:iphone手机用数据线连接电脑后只能充电无法进行文件传输的解决方法介绍
环球信息:iphone手机用数据线连接电脑后只能充电无法进行文件传输的解决方法介绍 -
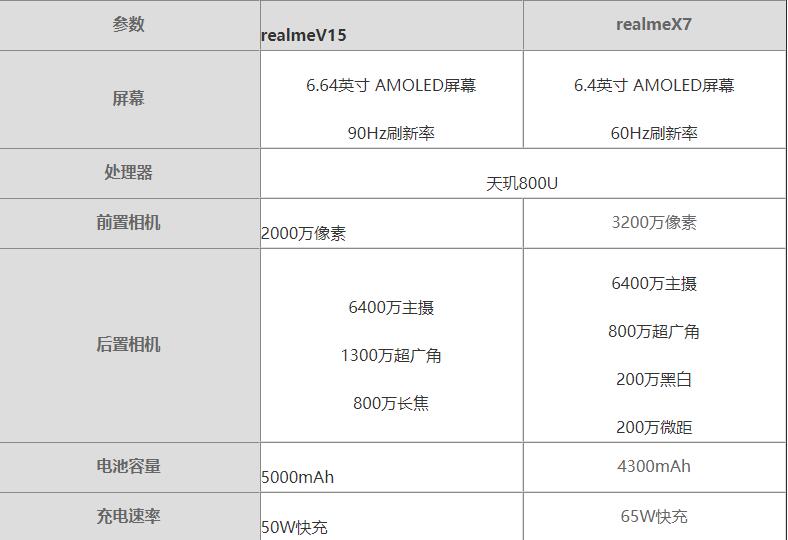 环球今热点:realmeV15对比realmeX7哪个好?realmeV15对比realmeX7评测
环球今热点:realmeV15对比realmeX7哪个好?realmeV15对比realmeX7评测 -
 当前视点!iOS 8.4 正式版发布 iOS 8.4到底升不升级?
当前视点!iOS 8.4 正式版发布 iOS 8.4到底升不升级?
精彩推荐
- Win11发布预览版更新:新版文件管理器绝了
- AMD 锐龙 8000处理器 正式确认: IPC增幅高达19%!
- 环球即时看!AMD Zen4c 霄龙细节曝光:升级4nm,128核心256线程碾压一切!
- 今日热闻!AMD Zen5 架构处理器数据疑似曝光, 锐龙 8000 系列要来了?
- 每日讯息!ICT中国·高层论坛|移动物联网高质量发展论坛在京举办
- 环球观点:华为发布100%自主数据库:数据安全有保障了
- 每日快报!苹果头显成本只有43%?
- 238 层 4D NAND 闪存量产,国产手机或率先使用,传输速度每秒 2.4Gb-每日视点
- 当前信息:比希捷便宜 西数推出XBOX存储扩展卡
- 全球今日报丨露营看片高画质:LG推出便携显示器
超前放送
- cakes什么意思 可以指蛋糕或蛋...
- 环球视讯!张学友电影 曾凭《泪...
- 教学相长的读音和解释 这个词的...
- 佛山一考生第一天走错考场:第二...
- 每日快报!3部韩国爆笑喜剧电影!...
- 教你轻松看懂八卦图 现在一般用...
- 做系统的步骤讲解 让我们看一看...
- 古墓丽影三部曲游玩顺序 线性的...
- 世界热点评!rs232是什么接口 ...
- 骁龙660处理器怎么样 骁龙660相...
- 首个文心千帆大模型平台在无锡成...
- 【环球报资讯】试验检测工程师考...
- 环球观速讯丨菱形面积公式 为何...
- WordPress 引入人工智能写作助...
- 古墓丽影9攻略图解 古墓丽影9的...
- 环球快看点丨快来看看瓦屋山旅游...
- 麻瓜是什么意思:麻瓜的意思是非...
- 当前资讯!罗素悖论及其他 辛普...
- 全球焦点!笔记本的主流配置 现...
- 高尔夫汽车怎么样:大众高尔夫性...
- 天天关注:牵手门女子同款裙子销...
- 刘邦的太子是哪一个 汉高祖刘邦...
- 世界标准时间 美国使用的标准时...
- 面点的制作方法 学会了做给家人...
- 中国瘦人增肥网 _增肥方法和增...
- 魔道学者觉醒叫什么名字 成功几...
- 原版红警单机手游怎么玩 向玩家...
- 炫舞魅力值等级怎么提升 在装备...
- 不同段位的游戏玩家 618大促告...
- 最适合毕业旅行的9个地方 和闺...
- 微动态丨0769是哪个城市的区号 ...
- 每日热议!花卉养殖技巧 浇花的...
- bus的复数形式怎么写?以辅音字母...
- 大象用英语怎么说 为何大象在印...
- 观叶秋海棠的养殖方法 栽培秋海...
- 化眼妆步骤 简单的眼妆画法 双...
- 超详细的学开车步骤 如果没有障...
- 简阳:突出重点抓汛期防范 力求...
- csgo开箱好还是买好?csgo凌晨开...
- 全球信息:“暑运”也可购得特价...
- 恩典qq透明皮肤高清原图 非主流...
- 造梦西游3八戒技能 热心玩家给...
- 安卓14终于更新:更更更丝滑了
- 天界徽章 Dnf天堂徽章主要用于...
- 新古典主义音乐 最重要的代表是...
- 环球热点!惊蛰的蜇读什么 英文...
- 邓超演的电视剧有哪些 幸福像花...
- 【世界独家】水浒传书中经常出现...
- 环球实时:合成皮革是什么材质 ...
- 5.5G预计2025年实现商用 网速比...









