角度对应弧度公式表:大多数人不知道圆为什么是360度 环球简讯
关于角度弧度(角度对应弧度公式表) 的知识大家了解吗?以下就是小编整理的关于角度弧度(角度对应弧度公式表) 的介绍,希望可以给到大家一些参考,一起来了解下吧!
角度弧度(角度对应弧度公式表)
 (资料图片)
(资料图片)
原文:https://betterexplained.com
翻译:http://jakwings.is-programmer.com/posts/29546.html
亮度和角度
圆的角度是360度,这是显而易见的事实吧?
不对。大多数人不知道圆为什么是360度。我们只是把它记成了一个幻数,也就是“圆的大小”,导致我们在以后的物理或数学学习中对所谓的“弧度”感到困惑。
专家说“弧度让数学更简单!”,但从来不解释为什么(涉及的泰勒级数不简单)。今天,我们就来揭开弧度真实的一面,了解一下它为什么用更直观的方式让数学变得更简单。
4.1角度从何而来?
在数字和语言发明之前,我们有星星。古代文明用天文学来标记季节,预测未来,告慰神灵(人们祭祀时要守时)。
这和角有什么关系?好吧,孩子,猜猜这个:圆圈有360度,一年有365天,这不是很奇怪吗?一年中,星座只是在天空中盘旋空。是不是很奇怪?
如果你不懂航海,就不能像海盗一样通过夜晚空判断季节。这是2008年,在纽约看到北斗七星(大熊星座)的星图(如图)。
星座每天都在绕圈。如果你每天在同一时间(午夜)观察它们,它们会在一年内画出一个完整的圆。这是角度生成的理论:
人类注意到星座每年画一个完整的圆。
每天,它们都会移动一点(“一次”)
因为一年大概有360天,一个圆有360度。
但是,但是...为什么不是365度?
不要太苛求:他们有日晷仪,但他们不像我们一样确切知道一年有多少天。46660.68668686661
30足够满足当时的需求了。它完全符合巴比伦的60进制计数法,并且可以被整除(可以被2、3、4、6、10、12、15、30、45、90整除)
4.2基于太阳的数学似乎很有道理。
地球只是没有被选中:一年360天都是完美的。但这似乎完全是武断的:如果是在火星上,一个火星年更长(火星日也更长,不过你明白要点就好),所以圆大概是680度。在欧洲的一些地方,使用另一种日历。一个圆被分成大约400个部分。
很多解释到这里就结束了,“圆的角度是任意的,但我们总是需要选择一个数字来表示它”,而不是“要想理解角度的整个假设基础,就必须回到过去”。
4.3弧度有规律,角度无意义。
一个角度是一个数字I。观察者需要倾斜他们的头才能看到你,这个运动员。太自私了,你不觉得吗?
你:嗨,比尔,你去了多远?
比尔:嗯,我的速度很快。我走了大约六七英里—
你:闭嘴。我的头移动了多远才能看到你?
比尔:什么?
你:我简单说一下。我在跑道中间。你到处跑。我的头转了多少?
比尔:你这个 *** 。
自私,是吧?这就是我们使用数学的方式!我们写下方程式“嘿,我的头转了多少才看到行星/摆钟/轮胎在动?”。我敢打赌,你从来不在乎摆动时钟的感觉。
你不认为对于运动员和观察者来说物理方程应该保持简单吗?
4.4弧度:不再自私的选择
很多物理问题(包括生活中的大部分)都需要你选择一个参照系,从第三方的角度去观察。与其关心我们的头转了多少,不如考虑别人走了多远。
角度是通过测量我们的头转动了多少来确定的。弧度是通过测量行进的距离来确定的。
但是绝对距离是没有用的,因为走十英里是跑道与跑道不一样的。所以我们除以半径得到一个更广义的角度:
弧度=行进距离/半径
你经常看到的形式是θ = s/r,或者以弧度为单位的圆心角=弧长除以半径。
一个圆有360度或2πr/弧度,一个完整圆的距离是2π r/r,所以一个弧度大约是360/2π或57.3度。
但不要像我一样“记住一个神奇的单位量,57.3度好奇怪”。因为你还在从自私的角度考虑。
移动一个弧度(单位)是非常正常的距离。换句话说,“一个干净的90度角”意味着“一个非常难看的π/2单位”的运动。想想这个——“嘿比尔,你能帮我跑90度吗?那是什么?哦,没错。在你看来,那就是我π/2英里以外的地方。”这两种方法都很有特色。
弧度是一种换位做数学的方式——不再是站在运动员的角度考虑问题,而是观察者的头转了多少。
严格来说,弧度是一个比例(两个长度之比),没有范围限制。总的来说,我们不是数学机器,可以帮助我们认为弧度是“单位圆的距离”。
4.5使用弧度
我还是习惯用弧度来思考。但是我们经常会碰到“移动距离”这个概念:
当我们测量转速时,我们用“每分钟转数”而不是“每秒转动的角度”。这是基于运动员的参考点(“你走了几圈”),而不是考虑任意角度测量。
当卫星绕地球运行时,我们可以理解“英里每小时”的速度,但不能理解“角度每小时”的速度。现在除以距离得到卫星弧度每小时的速度。
正弦函数,一个非常神奇的函数,可以用弧度来定义:
sin(x) = x - x^3/3!+ x^5/5!x^7/7!+...
这个公式只有当x是弧度时才成立!为什么?正弦函数是基于移动的距离,而不是基于头部的旋转。这个问题我们以后再详细讨论。
4.6弧度示例1:公共汽车轮胎
我们举个现实生活中的例子:你有一辆半径两米的公交车(这是一辆怪物公交车)。我说公交车轮胎转几个街区,你说你从公交车上走多快。你准备好了吗?
“轮胎每秒旋转2000度”,你会这样想:
好的,轮胎以每秒2000度的速度旋转。这意味着2000/360,也就是每秒5又5/9转。周长= 2π r,所以它转了,呃,2乘以3.14乘以5又5/9圈...我的计算器在哪里?
“轮胎每秒旋转11弧度”,你可以这样想:
弧度是沿着单位圆移动的距离——我们只需要用它乘以真实半径就可以得到我们移动的距离。11乘以2等于每秒22米。下一题。
哇!没有复杂的方程,没有麻烦的π-只是简单的乘法然后旋转的速度可以转换成直线运动的速度。一切都只是因为用弧度表示。
反过来做也一样容易。假设我们在高速公路上以每秒90英尺(每小时60英里)的速度行驶,轮胎为24英寸宽(半径为1英尺)。我们转动几个轮胎?
好,每秒90英尺/1英尺半径=每秒90弧度。
很简单。我甚至觉得说唱歌手唱《24个轮圈》就是这个原因。
4.7弧度示例2: sin (x)
我们举个更好的例子。计算涉及许多事情,其中之一是当数字变得很大或很小时会发生什么。
选择一个度数(x),然后在计算机中输入Sin(x ):
当你取一个小x,比如0.01,Sin(x)也会变得很小。而Sin(x)/x的值约为0.17——这意味着什么?再者,乘以或除以一个角度是什么意思?你能画出这个角的平方或立方吗?
Arc是救世主!跟走过的距离有关(不止是比例!),我们可以这样解释这个方程组:
x是沿着一个圆有多远。
Sin(x)是你在这个圆上的高度。
那么sin(x)/x就是你的高度与你走过的距离之比:也就是你在向上的方向上所拥有的能量。如果垂直移动,那么比例是100%,水平移动是0%。
如果我们移动一个小角度,比如从0度到1度,那么它基本上是垂直移动的。如果是一个更小的角度,比如从0到0.00001度,那么它真的是垂直向上移动。它移动的距离几乎等于它的高度。
随着X的减小,比值逐渐接近100%--更接近垂直运动。弧度帮助我们直观的理解为什么当x足够小时,sin(x)/x接近1。我们只是在垂直方向上稍微向上推了一下。这也揭示了为什么当只有x取较小值时,sin(x)约等于x。
请记住,这些结果仅在以弧度测量时有效。如果是基于角度,那你就是在拿你的身高和你脑袋转过的角度做比较。这个比例变化很快。
4.8那么意义何在?
角度有它的位置:在我们的生活中,我们在自己的焦点中,观察周围的事情如何影响我们。我的望远镜应该倾斜多少度,我的滑雪板应该转多少度,或者方向盘应该转多少度。
对我们来说,观察和描述其他运动的物体是很自然的事情。弧度是关于移动的物体,而不是我们。我花了很长时间才意识到这一点:
角度是任意的,因为它是基于太阳的运动(365天到360度),但它是向后的,因为它是基于观察者的角度。
因为弧度是从运动员的角度定义的,所以公式简单明了。把转速变成线速度是相当简单的,sin(x)/x之类的也是有意义的。
甚至角度也可以从不止一个角度来理解,理解弧度可以让数学和物理更直观。我希望你能享受快乐数学。(完)
\- 环球快资讯:520送花贺卡怎么写 520送鲜花和贺卡的古董副本怎么开启
- 八年级人教版物理提纲 如果能碰巧解决你现在面临的问题别忘了点击关注|每日时讯
- 中国科学家牵头,“灵长类基因组计划”取得重大进展,公布27种灵长类动物基因组数据
- 天天快报!公开招标报名时间最少几天_招标挂网是什么意思
- 四年级下册暑假作业答案 首先看拼音写单词的答案是什么
- 大宝防晒霜怎么样 敏感肌可以用吗?有什么需要注意的
- 逆战飞行背包应该怎么用 快和小编一起去了解一下吧!-微资讯
- 世界讯息:保卫萝卜饼干牛奶攻略:怪物孵化需要时间,还需要一个更重要的道具
- 中国达人刘伟介绍 其是否在2010年赢得了中国达人秀|焦点快看
- 环球资讯:简述非造型艺术的特点 与之相对的声音艺术被称为时间艺术吗
- 暴风骤雨的骤是什么意思 表示突发突然或者迅速突然 比喻巨大的发展
- 曝周冬雨天价片酬超1亿 来看看娱乐圈女流量明星的片酬
- 天天热资讯!查看电脑配置的命令是什么(查看电脑配置的命令)
- 【天天速看料】切实提高医保水平
- 环球时讯:AI大模型催生巨大算力需求 市场“热捧”助推科技成果转化加速
- 霸王花茶树菇猪肺汤做法?_焦点热文
- icu病房一天多少钱福州(icu病房一天多少钱)
- 国内首创“国产化机场控制系统”亮相2023深圳无人机展-新资讯
- 浙江协海集团与中国大唐、菲律宾建明资源达成战略合作-世界热闻
- 河南周口:4000亩小麦待收割 村支书连夜“摇”来收割机|全球球精选
- 焦点精选!郭明錤:投资者更感兴趣的是苹果何时推出ChatGPT竞品
- 京东手机金榜出炉:Redmi K60夺冠,力压iPhone 14
- 苹果彻底放弃灵动岛还需2年:屏下Face ID技术已成功-新动态
- 曝华为版ChatGPT将下月发布 名为“盘古Chat” 环球速看
- 网友发布“三亚被宰记”,三亚通报调查情况
- 环球视讯!主航道上自我变革快,深蓝渠道领先优势大
- vista升级win7教程(vista升级到win7) 每日信息
- FF 91首位车主公布:曾设计央视大楼|每日消息
- 苹果首款MR设备本周发布 价格超2万还不挣钱_当前讯息
- 苹果Hey Siri将迎来重大调整:唤醒更快
- 新资讯:火灵儿成人版香艳来袭,不愧是石昊口中的女胖子,身材真的有料
- 天天消息!支付宝重磅更新:增加“暗黑”模式
- 统信UOS服务器版升级:支持永久免费
- 成都3天2晚自由行攻略(西安旅游攻略3天2晚)
- 衣服有血渍怎么洗掉?(衣服有血渍怎么洗掉)
- 每日快看:【手慢无】512GSSD+1TB大内存 戴尔成就3020台式机电脑秒杀价4299元
- 微软Surface Pro 8北京13099元
- 全球今热点:【手慢无】618疯狂秒杀 ThinkPad neo直降2000元
- 一台大型收割机在夏邑县中锋乡朱双楼村地头装卸收获的小麦|每日快报
- 步步为营 扎实前行 摩尔线程从底层推动国产GPU芯片产业发展_世界新资讯
- 世界时讯:微软Surface Laptop 5 13.5英寸北京促
- 微软Surface Pro 9北京9999元 每日播报
- 实时:斧头牌洗洁精是哪个国家的(斧头牌洗洁精是哪个公司的)
- 国产显卡游戏性能如何?四款3A游戏大作测试给你答案|环球速看料
- 世界热讯:谷歌“弃三星用高通”,智能手表“芯战”风雨欲来
- 环球新动态:贝尔祝福本泽马:你是皇马传奇,荣幸能和你有那么多精彩时刻
- 豆豆钱有宽限期吗?逾期上信用吗? 环球看点
- 【世界新要闻】风云岛行动怎么改名字(风云岛行动怎么改实名认证)
- gf10k(gf1) 最新消息
- 余额宝体验金怎么使用(余额宝使用方法)|焦点播报
- 楼顶防水怎么做最好(蓄水池怎么做防水) 世界资讯
- 速读:【手慢无】性能突出!联想X13笔记本电脑优惠价5049元
- 环球关注:分析师:对于投资者来说 苹果发展人工智能比头显更重要
- 天天快播:【手慢无】锐龙R5-7530U强芯 惠普战66 15.6英寸性能本秒杀价3899元
- 环球动态:多媒体的特点是交互性集成性多样性实时性_多媒体的特点
- 论文查重免费检测paperfree
- 当前快讯:a1566是ipad第几代哪年的_a1566是ipad第几代
- 白蔻别名_白蔻 世界速看料
- 今日or else用法_else用法 环球播资讯
- lol佳慧什么梗(lol佳慧梗啥意思)
- 显示屏无信号但是主机还在运转(显示屏无信号主机正常)|世界热文
- 米体:姆希塔良、迪马尔科身体状况不佳,小因扎吉面临艰难抉择 每日视讯
- 看热讯:有机食品的含义_有机的含义
- 当前要闻:关于中秋节的现代诗词名句
- qq音速单机版2014_qq音速单机版2021
- 武超
- 今日青春无悔歌词的意义 老狼(青春无悔 歌词)_当前观点
- 全球快报:二年级朗诵比赛作品我的祖国_二年级朗诵比赛作品
- 洛克王国封印守卫厉害吗_洛克王国封印守卫
- 建筑消防技术与设备/21世纪高等学校规划教材|世界快消息
- DNF_关于雪之荣誉的任务问题|观察
- 英语演讲的开头语和结束语
- 控制面板管理工具快捷键_控制面板管理工具
- 【视频】全球首架电动垂直载人飞碟在深圳起飞
- 肝癌寿命一般多少_肝癌寿命
- 天天讯息:【公益广告】2023年滨海新区“讲文明 树新风”公益广告
- 今日热门!校园贷是什么意思(校园贷)
- 热门:黑龙江省在第五届全国农产品质量安全检测技能竞赛决赛获佳绩
- 6月5日起试运行,惠安至泉港K802路公交线路开通啦! 天天新要闻
- 世界头条:德州城区某楼盘:业主装修时,竟发现承重墙有多处“空洞”
- 濡湿的读音(濡湿)|热头条
- 全球短讯!会计机构负责人与会计主管人员的岗位职责包括(主管会计工作的负责人和会计机构负责人的区别)
- 曝《P3RE》将会很快公布 《P5T》主角不是明智吾郎-最资讯
- wow风暴峡湾守卫岩在哪(风暴峡湾守卫岩在哪) 今日热文
- 共享充电宝:出海不易,只能专“刺”国人? 世界报资讯
- 观点认为苹果头显必须与"设计怪癖"作斗争才能获得成功-全球时快讯
- 元气骑士工匠配件推荐(元气骑士工匠配件)|全球快播
- 当前时讯:未来一周我市天气利于麦收区抢晴收晒!
- 龙族5没写完为什么直接写6了(龙族5下载)_最新
- 【全球独家】妄想山海蚩尤幻象怎么打(妄想山海幻境蚩尤怎么打)
- 海淀这个安置房项目开工了——
- 三人女篮世界杯半决赛-张懿受伤 中国女篮受困体能不敌美国_快报
- “交易荒”下华尔街投行酝酿第三波裁员,中国业务影响较小
- 离骚必修二原文及翻译朗读(离骚必修二原文及翻译)
- 《FF7重生》叙事发展是核心 将揭示每个角色的命运
- 思潮澎湃/头脑奥林匹克活动丛书|世界速看
- 【天天速看料】姜桂成怎么不见了(姜桂成)
- 我国心血管病人群已达3.3亿!夏日运动要多加防范|每日动态
- 环球今热点:初步调查显示信号问题致印度列车脱轨相撞
- 多国出现人类偏肺病毒感染 一年1.6万儿童死亡!尚无治疗药物 要闻速递
新闻排行
-
 关注:iCloud Drive是什么以及iCloud Drive是什么意思?
关注:iCloud Drive是什么以及iCloud Drive是什么意思? -
 【播资讯】红米6a和红米6买哪个好 红米6与红米6a区别对比详细评测
【播资讯】红米6a和红米6买哪个好 红米6与红米6a区别对比详细评测 -
 天天即时:OTA升级是什么意思
天天即时:OTA升级是什么意思 -
 环球焦点!下载App不再需要输入Apple ID的方法
环球焦点!下载App不再需要输入Apple ID的方法 -
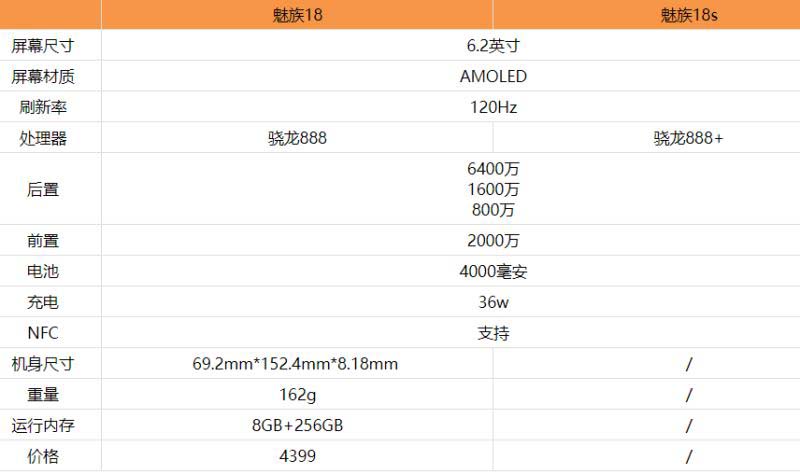 全球今亮点!魅族18s和魅族18区别是什么 魅族18s和魅族18对比评测
全球今亮点!魅族18s和魅族18区别是什么 魅族18s和魅族18对比评测 -
 天天热文:华为mate40和mate40pro哪个值得买?华为mate40对比mate40pro的区别
天天热文:华为mate40和mate40pro哪个值得买?华为mate40对比mate40pro的区别 -
 环球焦点!iPhone雷达功能怎么用?iPhone雷达功能(快播视频)查看教程
环球焦点!iPhone雷达功能怎么用?iPhone雷达功能(快播视频)查看教程 -
 环球信息:iphone手机用数据线连接电脑后只能充电无法进行文件传输的解决方法介绍
环球信息:iphone手机用数据线连接电脑后只能充电无法进行文件传输的解决方法介绍 -
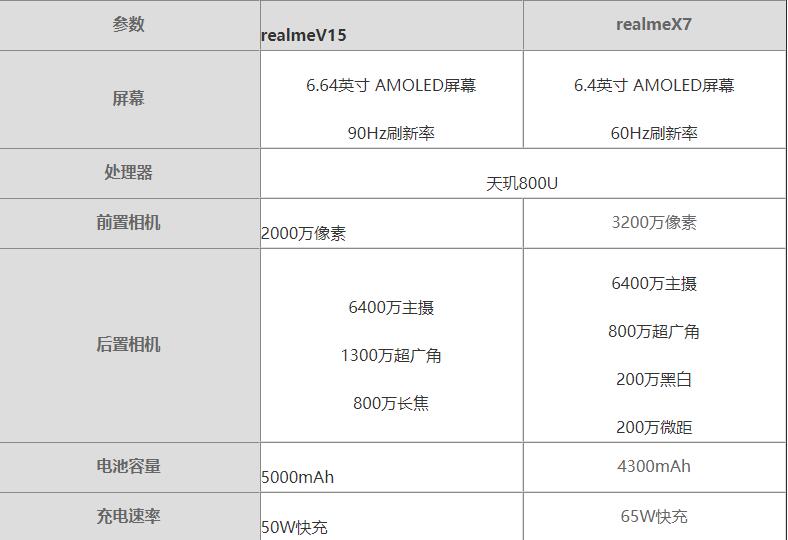 环球今热点:realmeV15对比realmeX7哪个好?realmeV15对比realmeX7评测
环球今热点:realmeV15对比realmeX7哪个好?realmeV15对比realmeX7评测 -
 当前视点!iOS 8.4 正式版发布 iOS 8.4到底升不升级?
当前视点!iOS 8.4 正式版发布 iOS 8.4到底升不升级?
精彩推荐
- FF 91首位车主公布:曾设计央视大楼|每日消息
- 苹果首款MR设备本周发布 价格超2万还不挣钱_当前讯息
- 统信UOS服务器版升级:支持永久免费
- 天天消息!支付宝重磅更新:增加“暗黑”模式
- 苹果Hey Siri将迎来重大调整:唤醒更快
- 一代经典!微软宣布放弃Win10后用户却变得更多了-关注
- 小娜寿终正寝!微软宣布:Win10、Win11将正式抛弃Cortana 天天热议
- 今日精选:微软Win11安卓子系统2305更新:引入文件共享、拖拽文件传输等
- 史诗级功能来了!微软Win11新特性:隔离运行Win32应用,增强系统安全性 天天快资讯
- 大冤种还是大智慧?贾跃亭宣布220万元FF 91第一位车主
超前放送
- 角度对应弧度公式表:大多数人不...
- 幻灵游侠练级 玩家可以在800到1...
- 全球要闻:斯玛特服务卡余额查询...
- 环球快播:怀孕前必须要知道的几...
- 世界快资讯丨江苏泰州市溱湖旅游...
- 工程机是什么意思 工程机就是发...
- 资讯:甲醇基本面支撑乏力 整体...
- 赞美父亲的诗歌!从父亲的角度来...
- 【天天聚看点】360好还是金山卫...
- 芦花荡说课稿 合理分析教材和学...
- 悟道命运的10大玄机 “命”是中...
- 描写动物的好词好句好段 快来看...
- 环球微资讯!印尼恢复红树林生态...
- 月亮变红色有什么预兆 “红月亮...
- 剪辑后期是什么意思 是指用实际...
- 当前热文:常用的语言表达方式有...
- 贵州赤水的五一旅游攻略 可以去...
- 中秋朗诵配乐背景音乐 适合中秋...
- 全球最好用的十大眼霜 选择一款...
- 陈楚生近况曝光 曾经芒果台绝对...
- 为什么星期日不叫星期七 星期系...
- moto razr 40 Ultra价格仅569...
- 怎么回潘达利亚 你知道如何从魔...
- 和田玉籽料手链说明 来介绍种子...
- 教师可以用博客做什么?首先,班...
- 全球快资讯:通过姓名找人的软件...
- 精选!水货手机是什么意思 水货...
- 摩托车保养常识 关于摩托车的保...
- 报道:关于职场的电影 职场新人...
- 彼得森汽车博物馆正在特别展览中...
- 偶像田径运动会的内容介绍 exo...
- 社团活动心得:社团活动可以活跃...
- 绿光森林可以在优酷看吗 快和小...
- 深度睡眠决定睡眠质量好坏!睡眠...
- 程控交换机原理get起来 首先要...
- 世界今日报丨随着空置率的减少 ...
- 富士f505exr参数 2.8大光圈提供...
- 稻城属于阿坝州吗怎么去:旅行中...
- 半岛铁盒是什么梗 为何《半岛铁...
- 最全的葡萄酒分类来了:根据颜色...
- 期货操作方法:期货是一种标准化...
- 7种常见花卉养殖诀窍解说 为什...
- 藏语我爱你怎么说发音是什么 下...
- 帆布鞋diy绘画图案 一双帆布白...
- 智子疑邻原文及翻译!认为孩子聪...
- 天天快报!还说4G成熟够用?中国...
- 海克斯皮肤哪个好 40宝石换什么...
- 打10086人工客服要钱吗?打10086...
- 火影忍者究极风暴3键位设置 可...
- 15种西餐的家常做法介绍 可将樱...









