自然数集符号 一般指一组非负整数 非负整数集也是可数集
在生活中,很多人都不知道自然数集(自然数集符号) 是什么意思,其实他的意思是非常简单的,下面就是小编搜索到的自然数集(自然数集符号) 相关的一些知识,我们一起来学习下吧!
今天和大家分享一下关于自然数集(自然数集符号)的问题。以下是小编对这个问题的总结。让我们看一看。
 (资料图)
(资料图)
一、什么是自然数集?
二。什么是自然数集?
自然数集一般指一组非负整数。
非负整数 *** 是一个特定的 *** ,指所有自然数的 *** ,通常用符号n表示,非负整数包括正整数和零,是一个可数 *** 。
所有非负整数的 *** 通常称为非负整数集(或自然数集)。非负整数集包含0、1、2、3等自然数。数学上,粗体的大写字母“n”表示一组非负整数。非负整数包括正整数和零。非负整数集是可数集。
自然
1.在非负整数 *** 中,有一个最小自然数为0;N去掉零后,由其他自然数组成的数集称为正整数集,通常用符号N+或N*表示,1是N+中最小的元素;N和N+中没有更大自然数;都是无限 *** 。
2.自然数1通常称为单位。
3.在N和N+中,取任意一个数,加上单位1。得到的号码称为该号码的后继号码。从最小的元素开始,一个一个加1。如果你无限地继续下去,你可以得到这个数集中的所有其他元素。最小元素不是任何元素的后继编号。
4、1可被任意自然数整除,其商仍是原自然数,所以1是任意自然数的除数。
5,0加任意自然数,其和仍是原自然数,1乘以任意自然数,其积仍是原自然数,所以所有自然数都是1的倍数。
6,1既不是质数,也不是合数。
7.如果0具有属性p,那么任何具有属性p的自然数的后继数都具有属性p..
8.非负整数 *** 中的数可以按顺序逐个计数,所以自然数 *** 是可数 *** 。
9.非负整数 *** 中的任意两个元素都可以进行大小比较,所以自然数 *** 是有序 *** 。
10.在非负整数 *** 中,加法和乘法总是可以实现的,即非负整数的和与积仍然是非负整数。
11.非负整数 *** 中的加法和乘法运算充满了* *交换律、结合律和乘法对加法的分配律。
12.非负整数 *** 中的加法和乘法满足消去律。
13.非负整数 *** 的任何non 空子集中必须有一个最小非负整数。这个结论被称为最小数原理。
三。什么是自然数集?
自然数集是所有非负整数的 *** ,通常用n表示,自然数有无穷多个。
扩展数据
自然数是所有等价有限集的共同特征的标志。
注意:整数包括自然数,所以自然数必须是整数,非负整数。
但是,减法和除法的结果并不总是自然数,所以减法和除法在自然数集中并不总是有效。用来衡量事物数量或表示事物顺序的数字。也就是数字0,1,2,3,4,…所代表的数字。代表物体数量的数字称为自然数,自然数一个接一个,形成一个无限的集体。
有自然数集加法和乘法运算。两个自然数相加或相乘的结果仍然是自然数,也可以相减或相除。但是,减法和除法的结果并不总是自然数,所以减法和除法运算在自然数集中并不总是有效。自然数是人们已知的所有数中最基本的。为了使数系具有严格的逻辑基础,19世纪的数学家们建立了自然数的两个等价理论:序数理论和基数理论,使自然数的概念、运算和相关性质得到了严格的讨论。
(序数理论是意大利数学家g·皮亚诺提出的。他总结了自然数的性质,并用公理化方法给出了自然数的如下定义)
自然数集是指满足下列条件的 *** :
①n中有一个元素,标记为1。
②N中的每个元素都可以找到N中的一个元素作为它的后继元素。
③1是0的后继者。④0不是任何元素的后继者。
⑤不同的元素有不同的继承者。
⑥(归纳公理)N的任意子集M,若1∈M,且只要X在M中,则可推导出X的后继也在M中,则M = N。
基数理论将自然数定义为有限集的基数。这个理论提出,能够在元素之间建立一一对应关系的两个有限集有一个共同的数量特征,叫做基数。这样,所有单个元素 *** {x}、{y}、{a}、{b}等。有相同的基数,标记为1。类似地,在可以用两个手指建立一对一对应集的地方,它们的基数是相同的,表示为2,以此类推。自然数的加法和乘法可以用序数理论或基数理论来定义,两种理论下的运算是一致的。
自然数在日常生活中起着重要的作用,人们广泛地使用它们。自然数是人类历史上最早的数,在计数和计量中有着广泛的应用。人们经常使用自然数来标记或分类事物,如城市公交路线、门牌号、邮政编码等。
自然数是整数(自然数包括正整数和零),但整数不全是自然数,例如:-1 -2 -3......是整数而不是自然数。自然数是无限的。
所有非负整数的 *** 称为非负整数集,即自然数集。
计数物体时,所计数的1.2.3.4.5.6.7.8.9 …称为自然数。自然数有数量和顺序两种含义,分为基数和序数。
基本单位:计数单位:一、十、一百、一千、一万、十万。......
简而言之,自然数是大于等于0的整数。当然还有负数,小数,分数等。不包括在内。
参考资料自然数_百度百科
四。“自然数集”是什么意思?
自然数集是所有非负整数的 *** ,通常用n表示,自然数有无穷多个。
自然数是所有等价有限集的共同特征的标志。
注意:整数包括自然数,所以自然数必须是整数,非负整数。
自然数集是指满足下列条件的 *** :
①n中有一个元素,标记为1。
②N中的每个元素都可以找到N中的一个元素作为它的后继元素。
③1是0的后继者。
④0不是任何元素的后继者。
⑤不同的元素有不同的继承者。
⑥(归纳公理)N的任意子集M,若1∈M,且只要X在M中,则可推导出X的后继也在M中,则M = N。
扩展数据:
自然数在日常生活中起着重要的作用,人们广泛地使用它们。自然数是人类历史上最早的数,在计数和计量中有着广泛的应用。人们经常使用自然数来标记或分类事物,如城市公交路线、门牌号、邮政编码等。
自然数是整数(自然数包括正整数和零),但整数不全是自然数,例如:-1 -2 -3......是整数而不是自然数。自然数是无限的。
所有非负整数的 *** 称为非负整数集,即自然数集。
计数物体时,所计数的1.2.3.4.5.6.7.8.9 …称为自然数。自然数有数量和顺序两种含义,分为基数和序数。
基本单位:计数单位:一、十、一百、一千、一万、十万。......
简而言之,自然数是大于等于0的整数。当然还有负数,小数,分数等。不包括在内。
元素具有以下属性:
1.确定性:每个对象都可以确定它是否是一个 *** 的元素。没有确定性,就成不了套。比如“高的同学”和“小的数”就不能形成一套。这个性质主要用来判断一个 *** 是否能构成一个 *** 。
2.异构性:一个 *** 中的任意两个元素都是不同的对象。
3.无序:在一个 *** 中,每个元素的状态是一样的,元素是无序的。可以在 *** 上定义顺序关系。定义了顺序关系后,可以根据顺序关系对元素进行排序。但就 *** 本身的特征而言,元素之间并没有必然的顺序。
以上就是上面小编关于自然数集(自然数集符号)及相关问题的回答。希望自然数集(自然数集符号)的问题对你有用!
\- 电脑运行速度慢的解决方法 可以右键选择点击磁盘清理即可_每日头条
- 当前简讯:晶澳科技:目前公司量产P型组件效率已达21.9%,N型组件效率已达22.5%
- 期权交易平台有哪些?普通人可以通过两个渠道投资期权
- 天天消息!iphone6上市时间、价格及性能介绍:有哪些优质的性能吸引消费者
- 每日热门:成语饮鸩止渴是什么意思 这个习语起源于哪里 寓意是什么
- 诺基亚系列手机有哪些:诺基亚130主打超长待机一个月 每日消息
- 诺基亚6230报价及评测 是在2004年上市的一款手机 在电池方面非常出色|热头条
- 让夏季穿搭个性又有气质 牛仔单品的搭配可以这样穿
- 今日热议:炉石传说乱斗模式奖励一览 乱斗模式只要赢了就送经典卡包吗
- dx11怎么安装 需要以管理员账户运行然后安装dx11组件
- 当前视点!445端口入侵:如果nalt|grep22不监听端口22,说明服务没有启动
- 詹姆斯哈登目前总得分是多少 排在第二位的是斯蒂芬吗
- 动态焦点:柳州电信协助警方“团灭”GOIP诈骗窝点
- 西班牙留学签证被拒的原因 为什么银行的流水不达标也会被拒
- 职场中常听到的寒暄:和职场人打交道,总会有愉快的对话
- 叶倩文秋去秋来原版 真正优秀的作品往往会受到普罗大众的追捧|今日热文
- 零基础咖啡小白如何选购咖啡豆 检查咖啡豆是否新鲜的方法其实很简单_全球热资讯
- 电阻基础知识汇总 一般来说我们使用的就是这几种常见的电阻
- 全球微动态丨如何快速去除鱼尾纹 银耳汁涂在眼睛上可以去除鱼尾纹吗
- 660MW!国能陈家港电厂灵活性一体化智能控制技术研究与应用项目招标
- 儿童白细胞参考范围(儿童白细胞参考范围) 世界快播报
- 小米13Ultra橄榄绿图赏:绿色科技纳米皮尽显高级 天天看热讯
- 新《小飞侠》电视预告:黑人精灵泼洒奇怪粉末 每日焦点
- 焦点速讯:九阴真经网游广告(九阴真经网游)
- 日全环食20日上演 我国少数地区可观测到
- 焦点快看:CVPR 2023 | 达摩院REALY头部重建榜单冠军模型HRN解读
- oppo推出reno10 pro+具备先进的相机功能 天天新动态
- 滴滴自动驾驶货运Kargobot亮相上海车展
- 【手慢无】ThinkPad E15 2022款商务轻薄笔记本电脑优惠200元|世界动态
- 国家统计局:一季度金融业GDP同比增长6.9%
- 监听新标杆,精准复现创作之音,索尼发布首款专业开放式监听耳机MDR-MV1 天天报资讯
- 199元!小米游戏手柄发布:支持Steam、三模连接
- 环球新动态:农业农村部发布2023年国家农作物优良品种推广目录
- 聚焦:印小酷线上打印,让你感受“效、简、快”的打印服务
- 环球微资讯!融合感知加速自动驾驶 复睿智行携4D毫米波雷达首征上海车展
- 《灌篮高手》中文配音预告 樱木花道流川枫配音回归
- 世界观察:华为高戟:8K入户,加速打造超高清产业集群
- 安恒信息(关于安恒信息的介绍)-全球快资讯
- 抖音电商木青:火山引擎驱动商家生意增长_时讯
- 【手慢无】军规品质认证+12核酷睿处理器 华硕a豆14pro轻薄笔记本3969元
- 新开发的测试方法可以现场快速进行沙门氏菌检测 环球快资讯
- 养老院经营模式解析(养老院经营模式)
- 新发现的13边形"非周期性单瓦"解决了60年的数学之谜-全球头条
- Ookla最新报告:2023年第一季度上网速度最快的国家是?|天天微速讯
- 德甲-帕瓦尔破门克拉马里奇扳平 拜仁1-1霍芬海姆
- 【手慢无】性价比太给力!巅峰玩家玄元V6游戏本仅售5199元-新要闻
- 世界热议:西班牙研究发现耐药细菌潜伏在40%的超市肉类中
- 观焦点:主播收入增长447%,近期视频号变现动作不断,创作者的机会在哪?
- 环球热点评!锐科激光与华工激光、柏楚电子、上海交大签署战略合作协议
- 【手慢无】满血4060独显!ThinkBook 16p 2023到手价9999!
- 【独家】走马灯是一种什么类型的灯泡(走马灯是一种什么类型的灯)
- 一季度投资消费外贸全面回暖
- 世界看热讯:网飞游戏用户参与度低迷 公司将在年内推出40款游戏
- 全球聚焦:外媒:Meta本周将再裁员4000人
- 咽喉有异物怎么处理(咽喉有异物怎么弄出来)_环球观速讯
- 雷军推荐小米6“钉子户”升级小米13系列 每日简讯
- AI炒股真来了?研究表明ChatGPT可解读美联储声明并根据新闻预测股票走势|世界球精选
- 《异度之刃3》最终DLC正式公布!4月26日推出
- 【环球聚看点】洛阳正大文化交流中心正式开放营业
- 环球焦点!意大利监管机构:若 OpenAI 采取「有效措施」 ChatGPT 有望 4 月 30 日重新上线
- 数据安全概念股异动拉升,汇纳科技涨超10%
- 当前消息!十大使用人工智能工具轻松赚钱的方法
- 欧洲成立人工智能研究中心来监督大型平台
- 苹果在印度继续扩张?库克将会见印度总理莫迪
- 迎趋势 创共赢 花王云客上线暨花王小幸福牌盛沛露酒上市发布会成功举办
- 日版iphone5s如何解锁?苹果5S的PIN初始密码一般是多少?
- 环球快讯:摆摊卖烤肠真的能月入百万吗?
- 篮球火第二部全集(篮球火第二部)-全球焦点
- 今年首季度PS5欧洲销量同比暴涨369% 《生化4重制版》获3月销冠
- 天天简讯:79元 小米米家多功能充电台灯发布
- 环球精选!小米13 Ultra预售秒罄!卢伟冰预言成真:1TB版被抢爆了
- 15万的宝马1系销量腰斩:国人更理性了?
- 时讯:梦幻胡姬琵琶行副本攻略(胡姬琵琶行副本攻略)
- 国产迷你主机白菜价:688元超值
- 28.89万起!新一代宝马X1上市
- 环球热讯:曾逃离北上广深的年轻人又回来了 适应不了小镇生活
- 马拉松等体育赛事陆续开启 京东携智能手表等潮电陪你科学运动
- 当前播报:爱国者2TB SSD售价仅579元 速度可达7450MB/s
- 兰博基尼、法拉利、宾利高管组团参观比亚迪仰望车展-世界热讯
- ChatExcel AI 办公辅助工具:通过文字聊天操控 Excel 表格|世界快播报
- 【当前热闻】甘肃省印发2023年法治政府建设工作要点
- 小米13 Ultra、iPhone 14 Pro Max实拍对比_热头条
- Midjourney王座不稳!Stable Diffusion-XL开启公测:可生成高质量图像 环球快播
- 赏花游热度攀升 京东电脑数码好物6期免息伴你共赴春日盛宴|快消息
- 世界即时看!重庆暴雨导致地铁站内积水 官方:不影响列车运行
- 这份周末出游攻略快收下! 荣耀手表2等硬核装备尽在京东电脑数码 今头条
- 环球最资讯丨华硕笔记本x84h报价 华硕x84h报价参考价格在4200元左右
- 天天消息!联想Y450TSI这款笔记本怎么样 联想Y450TSIH的优点和缺点是什么
- 富士S2000HD拍照怎么样:装备了一块2.7英寸23万像素的LCD_当前热门
- 三星S5830有什么好玩的单机游戏 三星S5830玩游戏怎么样?耗电快吗?
- 思量QQ透明皮肤V1.1官方免费版:使用这款修改器后不需修改任何QQ文件
- IESuper(IE超人)有哪些功能:最常见的增强功能广告过滤自然必不可少-世界速读
- 看热讯:苹果iphone4越狱教程 本文会教你如何做好准备工作
- 索尼CS36讲解:P机身采用了超薄设计,四周边角圆滑|热点评
- 索爱w705主题 在导航键和功能键的设计上与G705相似
- 金价再破历史纪录 2000美元/盎司大关已经被正式突破 天天微速讯
- 全球观天下!关于清明节的介绍 清明节融汇自然节气与人文风俗为一体 节俗丰富
- 怎么查上网记录及上网时间 教你查看宽带上网的时间|全球报道
- 每日头条!黑莓手机论坛网 黑莓9530手机拥有624MHZ的处理器
- 当前看点!联想g470_i5及2450对比 哪一个的显卡只是入门级别
新闻排行
-
 关注:iCloud Drive是什么以及iCloud Drive是什么意思?
关注:iCloud Drive是什么以及iCloud Drive是什么意思? -
 【播资讯】红米6a和红米6买哪个好 红米6与红米6a区别对比详细评测
【播资讯】红米6a和红米6买哪个好 红米6与红米6a区别对比详细评测 -
 天天即时:OTA升级是什么意思
天天即时:OTA升级是什么意思 -
 环球焦点!下载App不再需要输入Apple ID的方法
环球焦点!下载App不再需要输入Apple ID的方法 -
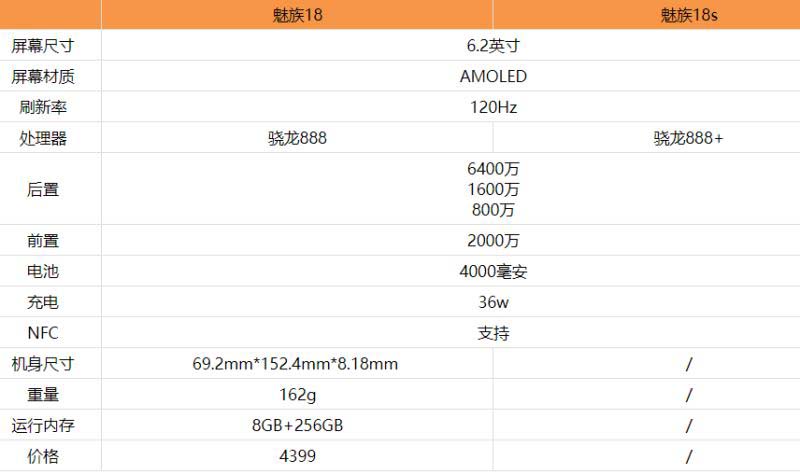 全球今亮点!魅族18s和魅族18区别是什么 魅族18s和魅族18对比评测
全球今亮点!魅族18s和魅族18区别是什么 魅族18s和魅族18对比评测 -
 天天热文:华为mate40和mate40pro哪个值得买?华为mate40对比mate40pro的区别
天天热文:华为mate40和mate40pro哪个值得买?华为mate40对比mate40pro的区别 -
 环球焦点!iPhone雷达功能怎么用?iPhone雷达功能(快播视频)查看教程
环球焦点!iPhone雷达功能怎么用?iPhone雷达功能(快播视频)查看教程 -
 环球信息:iphone手机用数据线连接电脑后只能充电无法进行文件传输的解决方法介绍
环球信息:iphone手机用数据线连接电脑后只能充电无法进行文件传输的解决方法介绍 -
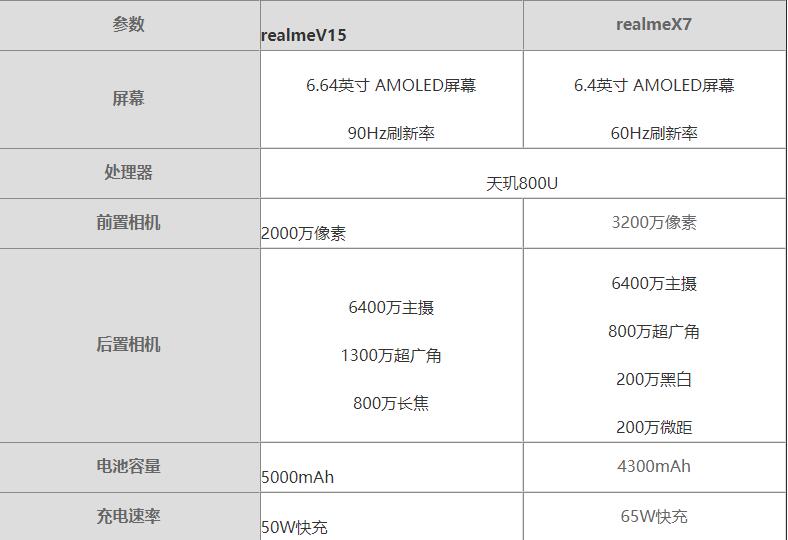 环球今热点:realmeV15对比realmeX7哪个好?realmeV15对比realmeX7评测
环球今热点:realmeV15对比realmeX7哪个好?realmeV15对比realmeX7评测 -
 当前视点!iOS 8.4 正式版发布 iOS 8.4到底升不升级?
当前视点!iOS 8.4 正式版发布 iOS 8.4到底升不升级?
精彩推荐
超前放送
- 每日信息:平方米等于多少公顷 ...
- 天天新资讯:阿波罗太阳神 一般...
- 修复浏览器怎么修 浏览器崩溃怎...
- 赛尔号怎么融合精灵 来解释一下...
- 每日信息:连笔字转换器 这个网...
- 对号错号怎么输入 怎么在excel...
- 自然数集符号 一般指一组非负整...
- windows7破解 带命令提示符的安...
- 怎么打开笔记本内置摄像头?为什...
- QQ默认的热键有哪些?QQ截图与其...
- 南京有什么地方好玩 南京博物馆...
- 屏息凝视到底是什么意思 就是屏...
- iphone7如何设置home键?苹果手...
- 全球报道:跳绳世界纪录:平均每秒...
- 三合一场所:指人员住宿场所与加...
- 手机淘宝怎么确认收货?淘宝怎么...
- 装系统后电脑没有声音怎么办?wi...
- 全网最全——丝带绣教程 如果你...
- cs龙珠该怎么玩如何操作 CS龙珠...
- psp游戏怎么安装?SONYPSP2000如...
- 最强大脑周玮后来怎么样了 情况...
- 网易163相册照片找回方法 网易...
- 热点评!宣传单尺寸一般多大 记...
- 电脑屏幕出现条纹是什么原因?手...
- 你知道国际圆周率日(Pi Day)吗...
- 英雄联盟fps忽高忽低怎么办?英...
- 电脑网卡灯不亮怎么办?网卡指示...
- 天天快资讯:dota2暂停键和开始...
- 腾讯总部投诉中心电话 反馈意见...
- 维尔托德什么水平 曼奇尼世界系...
- PSP3000的UMD光盘是什么?PSP破...
- 普利制药:公司近期暂未接受美国...
- 大熊猫是熊科还是猫科动物 野生...
- 华硕x45v系列怎么样?华硕x45v笔...
- 如何开锁 有什么开锁技巧 你知...
- 音乐拼接剪辑软件有哪些 Goodhe...
- 观赏龟种类大全图 巴西龟又名红...
- 钢琴硬件音源 MidiPiano是虚拟...
- iOS13.4耗电快怎么办?ios14和io...
- avi播放器哪个好用 应该怎么动...
- 艺术字体打包下载 希望有需要的...
- 揭开地铁楼兰姑娘的神秘面纱 只...
- fmea是什么意思 可用于识别吗 ...
- 网络机顶盒什么牌子好?什么牌子...
- 洗颜专科好用么 什么产品既能卸...
- 全球球精选!asp论坛源码免费版...
- 快播开启快播云加速无反应怎么办...
- win10输入法切换不了怎么办?win...
- 电脑网卡驱动安装不上怎么办?网...
- win7电脑提示系统保留分区未分配...










