з„ҰзӮ№е…іжіЁпјҡиҝҗзӯ№еӯҰеҚ•зәҜеҪўжі•жӯҘйӘӨиҜҰи§Ј дјҳеҢ–й—®йўҳзҡ„жӣҙдјҳи§ЈдёҖе®ҡжҳҜеҹәеҸҜиЎҢи§Ј
еңЁз”ҹжҙ»дёӯпјҢеҫҲеӨҡдәәйғҪдёҚзҹҘйҒ“иҝҗзӯ№еӯҰеҚ•зәҜеҪўжі•пјҲеҚ•зәҜеҪўжі•еҗ„дёӘжӯҘйӘӨиҜҰи§Јпјү жҳҜд»Җд№Ҳж„ҸжҖқпјҢе…¶е®һд»–зҡ„ж„ҸжҖқжҳҜйқһеёёз®ҖеҚ•зҡ„пјҢдёӢйқўе°ұжҳҜе°Ҹзј–жҗңзҙўеҲ°зҡ„иҝҗзӯ№еӯҰеҚ•зәҜеҪўжі•пјҲеҚ•зәҜеҪўжі•еҗ„дёӘжӯҘйӘӨиҜҰи§Јпјү зӣёе…ізҡ„дёҖдәӣзҹҘиҜҶпјҢжҲ‘们дёҖиө·жқҘеӯҰд№ дёӢеҗ§пјҒ
 (иө„ж–ҷеӣҫ)
(иө„ж–ҷеӣҫ)
иҝҗзӯ№еӯҰзҡ„еҚ•зәҜеҪўжі•(еҚ•зәҜеҪўжі•жҜҸдёҖжӯҘзҡ„иҜҰз»Ҷи§ЈйҮҠ)
rвҖңеҺҹеҲӣвҖқ
дҪңиҖ…:иҮ§ж°ёжЈ®
дҪңиҖ…з®Җд»Ӣ:иҮ§ж°ёжЈ®пјҢжё…еҚҺеӨ§еӯҰе·Ҙдёҡе·ҘзЁӢзі»еҚҡеЈ«з”ҹгҖӮз ”з©¶ж–№еҗ‘дёәиҝҗзӯ№еӯҰдјҳеҢ–з®—жі•зҡ„и®ҫи®ЎдёҺеә”з”ЁгҖҒж•°жҚ®зҡ„з»ҹи®ЎеҲҶжһҗгҖҒеӨ§ж•°жҚ®жҠҖжңҜдёҺеә”з”ЁпјҢеӣўйҳҹдёәйҪҗВ·гҖӮ
зј–иҫ‘иҜ„и®ә/жіЁйҮҠ
жң¬ж–ҮеұһдәҺз”өеӯҗд№ҰгҖҠзәҝжҖ§и§„еҲ’гҖӢ第дёүз« еҚ•зәҜеҪўжі•зҡ„еҶ…е®№гҖӮеңЁдёҠдёҖзҜҮж–Үз« дёӯпјҢжҲ‘们д»Ӣз»ҚдәҶеҸҜиЎҢеҹҹгҖҒжӣҙдјҳи§ЈгҖҒеҸҜиЎҢи§ЈгҖҒеҹәжң¬и§ЈгҖҒеҹәжң¬еҸҜиЎҢи§Јзӯүеҹәжң¬жҰӮеҝөгҖӮеҜ№дәҺеҚ•зәҜеҪўжі•зҡ„д»Ӣз»ҚпјҢд№ҹйҳҗиҝ°дәҶе®ғ们д№Ӣй—ҙзҡ„е…ізі»(иҜҰи§ҒеҚ•зәҜеҪўжі•д№ӢеүҚзҡ„ж–Үз« )гҖӮеңЁе®ҡд№үдәҶиҝҷдәӣеҹәжң¬жҰӮеҝөеҗҺпјҢжҲ‘们е°ҶеңЁжң¬иҠӮи®Ёи®әеҚ•зәҜеҪўжі•зҡ„жҖқжғійҖ»иҫ‘е’ҢжұӮи§ЈжӯҘйӘӨгҖӮ
жҲ‘们已з»ҸзҹҘйҒ“дјҳеҢ–й—®йўҳзҡ„жӣҙдјҳи§ЈдёҖе®ҡжҳҜеҹәеҸҜиЎҢи§ЈпјҢйӮЈд№ҲеҰӮдҪ•жүҫеҲ°жӣҙдјҳеҹәеҸҜиЎҢи§Је°ұжҳҜдјҳеҢ–й—®йўҳзҡ„жұӮи§ЈжҖқи·ҜгҖӮеӣ жӯӨпјҢеҚ•зәҜеҪўжі•зҡ„жұӮи§ЈиҝҮзЁӢжҳҜдёҖдёӘдёҚж–ӯеҜ»жүҫеҸҳйҮҸеҹәзҡ„еҫӘзҺҜиҝӯд»ЈиҝҮзЁӢгҖӮжҜҸж¬Ўиҝӯд»ЈиҫҫеҲ°йҷҚдҪҺзӣ®ж ҮеҮҪж•°еҖј(жҲ–еўһеҠ зӣ®ж ҮеҮҪж•°еҖј)зҡ„зӣ®зҡ„пјҢжңҖз»ҲиҺ·еҫ—жӣҙдјҳи§ЈгҖӮйӮЈд№ҲеңЁиҝӯд»ЈиҝҮзЁӢдёӯпјҢеҰӮдҪ•еңЁж”№иҝӣиҝҮзЁӢдёӯдҪҝи§Је°Ҫеҝ«ж”¶ж•ӣеҲ°жӣҙдјҳи§Је‘ўпјҹи®©жҲ‘们用жӣҙзӣҙи§Ӯзҡ„ж–№ејҸжқҘеҲҶжһҗиҝҷдёӘиҝҮзЁӢгҖӮ
еҚ•зәҜеҪўжі•зҡ„еҹәжң¬жҖқжғіе’ҢйҖ»иҫ‘
жң¬ж–ҮйҮҮз”Ёзҡ„жҖқи·ҜеҸӮиҖғдәҶDimitris Bertsimasе’ҢJohn N. TsitsiklisеңЁгҖҠзәҝжҖ§жӣҙдјҳеҢ–еҜји®әгҖӢдёҖд№ҰдёӯжҸҗеҮәзҡ„ж–№жі•[1]гҖӮиҖғиҷ‘д»ҘдёӢж ҮеҮҶзәҝжҖ§и§„еҲ’й—®йўҳ:
жҲ‘们жҠҠзҹ©йҳөAжӢҶеҲҶжҲҗNдёӘеҲ—е…ғзҙ :A1пјҢA2пјҢA3пјҢпјҢAnпјҢйӮЈд№ҲжҲ‘们е°ұеҸҜд»ҘжҠҠй—®йўҳзңӢжҲҗжҳҜж»Ўи¶ійқһиҙҹзәҰжқҹ(4)пјҢеҮёзәҰжқҹ(3)пјҢзәҰжқҹ(5)зҡ„жһҒе°ҸеҢ–й—®йўҳгҖӮ
з»“еҗҲж–№зЁӢ(3)е’Ң(5)еҸҜд»ҘзңӢеҮәпјҢеҺҹдјҳеҢ–й—®йўҳиҪ¬еҢ–дёәжұӮи§ЈиғҪжһ„йҖ (bпјҢz)并дҪҝzеҖјжңҖе°Ҹзҡ„(AiпјҢci)зҡ„еҮёз»„еҗҲгҖӮдёәдәҶжӣҙеҘҪзҡ„зҗҶи§Је®ғ们д№Ӣй—ҙзҡ„еҮ дҪ•е…ізі»пјҢжҲ‘们жҠҠдёҖдёӘе№ійқўзңӢдҪңеҢ…еҗ«Aзҡ„Mз»ҙз©әз©әй—ҙпјҢжҠҠдёҺciзӣёе…ізҡ„д»Јд»·йЎ№зңӢдҪңдёҖз»ҙзҡ„з«–ж•°иҪҙгҖӮжӯӨж—¶пјҢжҜҸдёӘзӮ№(AiпјҢci)йғҪеҸҜд»ҘеңЁиҝҷдёӘдёүз»ҙеқҗж Үзі»дёӯе”ҜдёҖиЎЁзӨәпјҢеҰӮеӣҫ1жүҖзӨә:
еӣҫ1зәҝжҖ§и§„еҲ’й—®йўҳ1-4зҡ„вҖңеҲ—еҮ дҪ•вҖқеӣҫ
жҲ‘们д№ҹжҠҠ(bпјҢz)зңӢдҪңеӣҫ1дёӯзҡ„дёҖжқЎеһӮзӣҙзәҝгҖӮиҝҷжқЎеһӮзӣҙзәҝз§°дёәйңҖжұӮзәҝпјҢе®ғдёҺе№ійқўзҡ„дәӨзӮ№жҳҜзӮ№(bпјҢ0)гҖӮйңҖжұӮзәҝдёҺ(AiпјҢci)зҡ„еҮёз»„еҗҲжңүдёҖе®ҡзҡ„еҮ дҪ•е…ізі»гҖӮе®ғ们иҰҒд№ҲзӣёдәӨпјҢиҰҒд№ҲиғҢзҰ»пјҢиҝҷеҸ–еҶідәҺжҲ‘们еҜ№(AiпјҢci)зҡ„еҮёз»„еҗҲзҡ„йҖүжӢ©гҖӮйҖүеҸ–зҡ„еҮёз»„еҗҲдёҚеҗҢж—¶пјҢеҮ дҪ•е…ізі»д№ҹдёҚдёҖж ·гҖӮеҫҲе®№жҳ“зҗҶи§ЈпјҢеҰӮжһңйңҖжұӮзәҝдёҺеҮёз»„еҗҲзӣёдәӨпјҢе°ұж„Ҹе‘ізқҖ(bпјҢz)еҸҜд»Ҙз”Ёзӣёеә”зҡ„еҮёз»„еҗҲжқҘиЎЁзӨәпјҢд№ҹе°ұжҳҜиҜҙиҝҷдёӘеҮёз»„еҗҲжҳҜеҺҹй—®йўҳзҡ„еҸҜиЎҢи§ЈгҖӮдҪҶеҰӮжһңжҠҠе®ғ们еҲҶејҖпјҢе°ұиҜҙжҳҺиҝҷдёӘеҮёз»„еҗҲдёҚж»Ўи¶іиғҪиЎЁзӨә(bпјҢz)зҡ„жқЎд»¶пјҢжүҖд»ҘдёҚжҳҜеҺҹй—®йўҳзҡ„еҸҜиЎҢи§ЈгҖӮжүҖжңүеҮёз»„еҗҲеҪўжҲҗдёҖдёӘеҮёеҢ…гҖӮеҰӮжһңйңҖжұӮзәҝиғҪдёҺеҮёеҢ…зӣёдәӨпјҢйӮЈд№ҲеҺҹй—®йўҳе°ұжңүеҸҜиЎҢи§ЈгҖӮеҰӮжһңйңҖжұӮзәҝдёҚиғҪдёҺеҮёеҢ…зӣёдәӨпјҢеҺҹй—®йўҳж— и§ЈгҖӮиҝӣдёҖжӯҘжҠҪиұЎеӣҫ1еҫ—еҲ°еӣҫ2гҖӮд»ҺеӣҫдёӯеҸҜд»ҘзңӢеҮәпјҢзӮ№IгҖҒHгҖҒGжҳҜдёүз§ҚдёҚеҗҢеҮёз»„еҗҲе’ҢйңҖжұӮзәҝзҡ„дәӨзӮ№пјҢжҳҜеҺҹй—®йўҳзҡ„дёүз§ҚеҸҜиЎҢи§ЈгҖӮ
еӣҫ2еҸҜиЎҢи§ЈеҶіж–№жЎҲзҡ„вҖңжҹұеҮ дҪ•вҖқеӣҫ
з»ҸиҝҮд»ҘдёҠеҲҶжһҗпјҢжҲ‘们зҹҘйҒ“пјҢиҰҒжүҫеҲ°жӣҙдјҳи§ЈпјҢе°ұжҳҜиҰҒжүҫеҲ°дёҺйңҖжұӮзәҝзӣёдәӨдё”дҪҝZеҖјжңҖе°Ҹзҡ„еҮёз»„еҗҲгҖӮйӮЈд№ҲеҰӮдҪ•жүҫеҲ°иҝҷж ·зҡ„еҮёз»„еҗҲе‘ўпјҹйҰ–е…ҲпјҢеј•е…ҘдёӨдёӘе®ҡд№ү:
еҰӮжһңзҹўйҮҸ
жҳҜзәҝжҖ§ж— е…ізҡ„пјҢйӮЈд№Ҳеҗ‘йҮҸ
иў«з§°дёәRnз©әй—ҙдёӯзҡ„д»ҝе°„зӢ¬з«ӢжҲ–иҖ…д»ҝе°„ж— е…іпјҢе…¶дёӯk
\- 专家жҢҮеҮә移еҠЁеә”з”Ёиҙ§еёҒеҢ–зҡ„дә”еӨ§иҜҜеҢә дё–з•ҢзғӯзӮ№
- е‘Ёжқ°дјҰе°ұдёҚжӯЈеҪ“з«һдәүиө·иҜүзҪ‘жҳ“пјҢ4жңҲ17ж—ҘејҖеәӯ|зҺҜзҗғеҫ®еҠЁжҖҒ
- дё–з•ҢеҠЁжҖҒ:еҺҶж—¶4иҪҪпјҢжҲ‘们жӣҙиҝӣдёҖжӯҘгҖӮ4жңҲ14еҸ·пјҢдёҖиө·и§ҒиҜҒйҮҸеӯҗи®Ўз®—зҡ„ж–°жңӘжқҘ
- iPhone15ProMaxйў„и®Ўе”®д»·2дёҮеқ— иӢ№жһң15ProMaxд»·ж јжӣқе…ү|зҺҜзҗғж’ӯиө„и®Ҝ
- 46еІҒжқҺе°ҸеҶүжҷ’жҙ»еҠЁзҫҺз…§ ејҖиЎ©й•ҝиЈҷж°”иҙЁдјҳйӣ… зҺҜзҗғзғӯй—»
- еӨ©еӨ©и§ӮеҜҹпјҡжҷҜеҢәйӘҶй©јиў«иҪ®з•ӘжЈ’жү“еұҲиҶқжұӮйҘ¶ зҪ‘еҸӢпјҡзңӢзҡ„еӨӘеҝғз–ј
- гҖҠжЎғжәҗж·ұеӨ„жңүдәә家гҖӢеҫ®дҝЎQQзҰҸеҲ©жҖҺд№ҲйўҶж–№жі•-д»Ҡж—Ҙзғӯй—Ё
- жө·дҝЎеҶ°з®ұз”ҳиӮғе®ҡиҘҝвҖңеҠ©еӯҰи®°вҖқ
- гҖҗе…Ёзҗғеҝ«ж’ӯжҠҘгҖ‘е°ҸзұіжҷәиғҪйҹійў‘зңјй•ңеҸ‘еёғпјҡж”ҜжҢҒйҖҡиҜқйҷҚеҷӘе’ҢIP54йҳІе°ҳйҳІж°ҙ
- еҝ«и®ҜпјҡзңҹжҲ‘GT Neo5 SEйҰ–й”Җпјҡ16GB 1TBд»…е”®2599
- 4жңҲ10ж—Ҙ12ж—¶еұұдёңеҫ·е·һжңүзЎ®иҜҠз—…дҫӢеҗ— 4жңҲ10ж—Ҙ12ж—¶еұұдёңеҫ·е·һз–«жғ…е®һж—¶жңҖж–°йҖҡжҠҘ
- гҖҗзҺҜзҗғж’ӯиө„и®ҜгҖ‘жғ жҷ®з¬¬9д»ЈжёёжҲҸ家ж—ҸйҮҚзЈ…еҸ‘еёғпјҢеҠ©еҠӣзҺ©е®¶гҖҢзҺ©еҮәеҶ…еҠӣ еҶҚжқҘдәҝжҠҠгҖҚ
- 2000MB/sи¶…й«ҳйҖҹиҜ»еҶҷпјҒHP P900й«ҳйҖҹ移еҠЁеӣәжҖҒзЎ¬зӣҳе…Ёж–°еҸ‘еёғ|е…Ёзҗғеҝ«ж’ӯжҠҘ
- еӨ©еӨ©жҠҘйҒ“:жҳҫзӨәиЎҢдёҡдәҢе·ЁеӨҙжө·дҝЎгҖҒе…үеі°е…ұжҺЁдёүиүІжҝҖе…ү иҝҷеҮ йЎ№дјҳеҠҝжҳҺжҳҫ
- гҖҗжүӢж…ўж— гҖ‘зӣҙйҷҚ600е…ғпјҒзҒ«еҪұRTX 4060жёёжҲҸжң¬и·Ңз ҙ6000
- е‘Ёжқ°дјҰе°ұдёҚжӯЈеҪ“з«һдәүиө·иҜүзҪ‘жҳ“ жң¬жңҲ17ж—ҘејҖеәӯ зҺҜзҗғж’ӯжҠҘ
- гҖҗжүӢж…ўж— гҖ‘зӣҙйҷҚ200е…ғпјҒиҚЈиҖҖBook X 16 Pro2023ж¬ҫ笔记жң¬з§’жқҖ4699е…ғ|еӨ©еӨ©и§ӮйҖҹи®Ҝ
- е°ҸзұіMIJIAжҷәиғҪйҹійў‘зңјй•ңеҸ‘еёғпјҒзӢ¬зү№иҖіжңәзңјй•ңдәҢеҗҲдёҖи®ҫи®Ў|еҪ“еүҚеҠЁжҖҒ
- з ”з©¶дәәе‘ҳеҸ‘зҺ°ең°зҗғеӨ§ж°”еұӮиҮӘжҲ‘жё…жҙҒзҡ„дёҖз§Қж–№ејҸ|еӨ©еӨ©зғӯеӨҙжқЎ
- зҹӯи®ҜпјҒжҡ—еҪұзІҫзҒө9жёёжҲҸ笔记жң¬еҸ‘еёғпјҡ13д»Јi9+RTX 4060 д»…8499е…ғ
- е®Ӣе…¬иҗ§зҰ№
- iPhone 15 Pro Maxйў„и®Ўе”®д»·2дёҮзҷ»йЎ¶зғӯжҗң зҪ‘еҸӢпјҡеҸӘеүІжңүй’ұдәәйҹӯиҸң-дё–з•ҢиҒҡзңӢзӮ№
- еҫ®йҖҹи®Ҝпјҡ4жңҲ10ж—Ҙ11ж—¶жұҹиҘҝд№қжұҹд»ҠеӨ©ж–°еўһзЎ®иҜҠеҗҚеҚ• 4жңҲ10ж—Ҙ11ж—¶жұҹиҘҝд№қжұҹз–«жғ…йҳІжҺ§ж”ҝзӯ–жңҖж–°йҖҡзҹҘ
- гҖҠеҘізҘһејӮй—»еҪ•3пјҡйҮҚеҲ¶зүҲгҖӢе·ІејҖеҸ‘еӨҡе№ҙпјҡжҲҳж–—з”»йқўжҲ–йҒӯжі„йңІ
- гҖҗжүӢж…ўж— гҖ‘з”өз«һеұҸ жғ жҷ®жҡ—еҪұзІҫзҒө9жёёжҲҸжң¬жҠўиҙӯд»·6999е…ғ
- жҖ§иғҪе°ұжҳҜжңҖеҘҪзҡ„йӯ”жі• OMENжҡ—еҪұзІҫзҒө9 Plusй«ҳиғҪзүҲдҪ“йӘҢгҖҠйңҚж јжІғиҢЁд№ӢйҒ—гҖӢ
- 科жҠҖзҡ„еҠӣйҮҸпјҒжі°еӣҪз”·еӯҗз”ЁChatGPTд№°еҪ©зҘЁдёӯеҘ–
- дё–з•Ңеҫ®иө„и®ҜпјҒйҖүеқҖдёҠжө· зү№ж–ҜжӢүе»әи®ҫMegapackе·ҘеҺӮ
- й”®зӣҳзҡ„Ctrl+WжҳҜд»Җд№Ҳпјҹз”өи„‘жҖҺж ·еҲҮжҚўиҫ“е…Ҙжі•пјҹctrlй”®ж— е“Қеә”жҖҺд№ҲеҠһпјҹ
- дәӨдәҶзӨҫдҝқдёҚдәӨеҢ»дҝқеҸҜд»Ҙеҗ— зҺҜзҗғеҝ«иө„и®Ҝ
- еӨ©еӨ©ж—¶и®ҜпјҡеҚҺдёәu8860и®әеқӣ еҚҺдёәиҚЈиҖҖu8860зҡ„е®Ңж•ҙеҲ·жңәж•ҷзЁӢжҳҜжҖҺж ·зҡ„
- е№ҝиҘҝйҫҷжұҹ:жҳҜеұһдәҺе№ҝиҘҝжЁӘеҺҝеіҰеҹҺй•ҮдёӢж»•жқ‘зҡ„дёҖдёӘи‘—еҗҚжҷҜзӮ№
- еүҚжІҝзғӯзӮ№пјҡAIGCжҠҖжңҜе‘ЁжҠҘпҪңеӣҫзҒөжөӢиҜ•дёҚжҳҜAGIзҡ„жҷәеҠӣж ҮеҮҶпјӣSegGPTпјҡеңЁдёҠдёӢж–ҮдёӯеҲҶеүІдёҖеҲҮпјӣChatGPTиғҪзҺ©еҘҪж–Үеӯ—жёёжҲҸеҗ—пјҹ
- дё–з•Ңеҝ«зңӢзӮ№дёЁе…үзҺҜдё»еҲӣзҰ»ејҖеҫ®иҪҜ
- 40е‘Ёе№ҙ жҳҹжҲҳ4жңҲ28ж—ҘеӣһеҪ’еҪұйҷўйҮҚжҳ пјҒ
- kb3132372еңЁе®үиЈ…жӣҙж–°ж—¶йҒҮеҲ°дәҶиҝӣеәҰеҚЎеңЁ30%зҡ„й—®йўҳ иҜҘеҰӮдҪ•и§ЈеҶі_еӨ©еӨ©дә®зӮ№
- е°ҸзұіжүӢжңәеҰӮдҪ•дҪҝз”ЁgmailйӮ®з®ұ еҰӮдҪ•еғҸз”өи„‘зҷ»йҷҶдёҖж ·ж”¶еҲ°йӘҢиҜҒз ҒдҝЎжҒҜ жҜҸж—Ҙеҝ«жҠҘ
- дҝЎй•ҝд№ӢйҮҺжңӣ13зү№е…ёжӯҰе°ҶдёәдҪ•зҷ»дёҚеҲ° еҰӮдҪ•жүҚиғҪи®ҫзҪ®еҘҪжёёжҲҸи·Ҝеҫ„
- е…Ёзҗғеҝ«ж¶ҲжҒҜпјҒеӨ§жҳҫжүӢжңәе®ҳзҪ‘зҪ‘еқҖжҳҜд»Җд№ҲеҰӮдҪ•жҗңзҙў еӨ§жҳҫжүӢжңәжҳҜе“Әз”ҹдә§зҡ„
- е…ідәҺжҜ•ж‘©зәӘзҡ„д»Ӣз»ҚдёҠзәҝ иҝҷжҳҜжқЁи•Ҡжү§еҜјзҡ„дёҖйғЁеү§жғ…з”өеҪұеҗ—_дё–з•ҢйҖҹзңӢ
- йЎөжёёд№ҹиғҪз”ЁжҳҫеҚЎ и°·жӯҢжҺЁеҮәWebGPU-дё–з•ҢиҰҒй—»
- зҺҜзҗғиҰҒй—»пјҡBз«ҷUWPзүҲе®ҳе®ЈеҒңжӯўз»ҙжҠӨпјҒXboxдёҠд№ҹдёҚиғҪз”ЁдәҶ
- еӨ©еӨ©и§ӮзӮ№пјҡз”өи„‘еҲҶжңҹд»ҳж¬ҫжҳҜжҖҺд№ҲеҲҶжңҹ иҰҒз”іиҜ·еҲҶжңҹд»ҳж¬ҫзҡ„иҜқиҜҘжҖҺд№Ҳж“ҚдҪң
- иӢҸе·һж–°жҷӢзҪ‘зәўз«№зӯ’еҘ¶иҢ¶ еҚ•жқҜжҷ®йҒҚи¶…30е…ғ
- f718жҳҜдёҚжҳҜеҸҢеҚЎ йЈһеҲ©жөҰF718йҮҮз”ЁйҮ‘еұһжңәиә«дјҡдёҚдјҡеҫҲйҮҚпјҹ_зҺҜзҗғжҠҘйҒ“
- жҙӣе…ӢзҺӢеӣҪжӨҚзү©еӣӯйҮҮиҠұд»»еҠЎж”»з•Ҙд»Ӣз»Қ еҝ«е’Ңе°Ҹзј–дёҖиө·еҺ»дәҶи§ЈдёҖдёӢ-д»Ҡж—Ҙзғӯи®Ҝ
- chinajoy cosplayеҳүе№ҙеҚҺе…ЁеӣҪеӨ§иөӣ иҺ·еҘ–зҡ„жңүеҠӣз«һдәүиҖ…йғҪжңүи°Ғ
- жһ—дҝҠжқ°еҸ‘ж–Үеӣһеә”д№°иҷҡжӢҹең°дә§жө®дәҸ91% 12.3дёҮзҫҺе…ғд»…еү©1дёҮзҫҺе…ғ-дё–з•Ңж–°и§ҶйҮҺ
- жүӢжңәж–°жөӘеҫ®еҚҡзҷ»дёҚдёҠеҺ»:еҸҜд»ҘеҲ йҷӨжүӢжңәдёҚеёёз”Ёзҡ„еә”з”Ё жё…зҗҶжүӢжңәеҶ…еӯҳ-зҺҜзҗғж–°ж¶ҲжҒҜ
- SpaceXиҝ‘жңҹйҰ–ж¬ЎиҜ•е°„жҳҹиҲ°
- NVIDIA GeForce 9300MеҸҠGSжҳҫеҚЎжҖҺд№Ҳж · жҺЁиҚҗжҢүдёӘдәәйңҖжұӮжқҘе®ҡжҖ§-еҪ“еүҚеҠЁжҖҒ
- е…ідәҺdell500зҡ„д»Ӣз»Қ жҳҜдёҖж¬ҫ15.4еҜёеӨ§еұҸ笔记жң¬ жҳҜ2008е№ҙзҡ„дҪҺз«ҜжңәеһӢ|дё–з•Ңиө„и®Ҝ
- NAB ShowпјҡMarshall дҪҝз”Ёж–°дј ж„ҹеҷЁеҚҮзә§ POV зӣёжңәзі»еҲ—
- е…ЁзҗғзңӢзғӯи®ҜпјҡжёҜзүҲiPhone6sж”ҜжҢҒиҒ”йҖҡ4Gеҗ—пјҹд»ҺзҪ‘з»ңеҲ¶ејҸдёҠжқҘзңӢиғҪеҸ‘зҺ°д»Җд№Ҳ
- жҜҸж—ҘйҖҹйҖ’пјҡBroadpeakжҺЁеҮәж–°дёҖд»Јй«ҳзә§CDN
- е…ідәҺеҺҰй—Ёдјҡи®®зӯ–еҲ’зҡ„д»Ӣз»Қ:д»Ҙдё“дёҡзҡ„дәәжҖ§еҢ–жңҚеҠЎдёәдә®зӮ№ з„ҰзӮ№дҝЎжҒҜ
- жҲҗйғҪеҚҮжё©еҚғи¶іиҷ«ж»ЎиЎ—зҲ¬ иҝҮж•ҸдҪ“иҙЁиҰҒе°ҸеҝғпјҒ еӨ©еӨ©йҖҹиҜ»
- гҖҗжүӢж…ўж— гҖ‘жҖ§д»·жҜ”ж— ж•ҢдәҶпјҒ23ж¬ҫжғ жҷ®е…үеҪұзІҫзҒө9зӣҙйҷҚ300е…ғ еӨ©еӨ©и§Ӯз„ҰзӮ№
- йў„з®—е……и¶іпјҒ1-2дёҮе…ғз”өи§ҶжҖҺд№ҲйҖүпјҹ
- е…ідәҺйҮ‘з§ҖиҙӨеҰ№еҰ№зҡ„д»Ӣз»Қ йӮЈдёӘеҙӯйңІеӨҙи§’зҡ„ж–°дәәеҘіжӯҢжүӢеҸ«д»Җд№Ҳ
- е…ідәҺе„ҝз«Ҙж–ҮеӯҰеӨ§жң¬иҗҘзҡ„д»Ӣз»Қ дёәе°‘е№ҙе„ҝз«ҘејҖжӢ“дёҖзүҮзәҜзҫҺзҡ„еӨ©ең°_и§ӮеҜҹ
- kmplayer_Divxи§Јз ҒеҷЁжү“дёҚејҖжҳҜз”ұдәҺиҪҜ件жң¬иә«зҡ„еҺҹеӣ еҗ—
- з”өи„‘зҺ©DNFдёҖзӣҙеҚЎеұҸжҖҺд№Ҳи§ЈеҶіпјҹз”өи„‘зҺ©dnfеҚЎжӯ»жҳҜд»Җд№ҲеҺҹеӣ пјҹ
- и§ӮеҜҹпјҡ360жөҸи§ҲеҷЁжү“дёҚејҖqqз©әй—ҙжҖҺд№ҲеҠһ иҜҘеҰӮдҪ•и§ЈеҶіиҝҷдёӘй—®йўҳ
- еӨ©еӨ©еҝ«зңӢзӮ№дёЁз”іиҜ·з”өиҜқеҸ·з Ғзҡ„ж–№жі•жңүе“Әдәӣ еҰӮжһңжҳҜеӣәе®ҡз”өиҜқиҜҘеҺ»е“ӘйҮҢејҖйҖҡ
- е…ідәҺеҢ—еҪұж ЎеәҶзҡ„д»Ӣз»Қ д»ҠеӨ©е°ұз»ҷеӨ§е®¶з§‘жҷ®дёҖдёӘзӣёе…ізҡ„е°ҸзҹҘиҜҶ|дё–з•ҢеҠЁжҖҒ
- жқҘзҺ©еҗ§йҹ©еӣҪз»јиүәеңЁе“ӘзңӢ еҳүе®ҫйҷӨдәҶйҮ‘еёҢжҫҲйҮ‘ж”ҝжЁЎд№ӢеӨ–иҝҳжңүи°Ғ|е…Ёзҗғж–°ж¶ҲжҒҜ
- иүҫиҜәиҝӘдәҡ4дҪЈе…өиҒҢдёҡе®ҢзҫҺжҗӯй…Қз»„еҗҲ жі•еёҲзҡ„жҠҖиғҪе…ЁйғҪжҳҜеўһеҠ ж”»еҮ»зҡ„еҗ—
- еҸҳеҪўйҮ‘еҲҡ2еҘідё»и§’жҳҜи°Ғ йҳҝе°”иҢңдёүе§җеҰ№йғҪеҲҶеҲ«жҳҜи°ҒйҘ°жј”зҡ„ дё–з•Ңж—¶и®Ҝ
- дёүжҳҹwb1000д»Ӣз»Қ:йҮҮз”Ёж–ҪиҖҗеҫ·и®ӨиҜҒй•ңеӨҙд»ҘеҸҠ5еҖҚе…үеӯҰеҸҳз„Ұ
- зәўзұіжүӢжңәеҸҜд»ҘжҚўз”өжұ еҗ—пјҹзәўзұіжүӢжңәжҚўз”өжұ еҗҺеҜ№жүӢжңәжңүд»Җд№ҲеҪұе“Қпјҹ
- е…ідәҺдёӯз§ӢиҠӮзҡ„д»Ӣз»ҚпјҡзҺ°е·ІжҲҗдёәдё°еҜҢеӨҡеҪ©гҖҒејҘи¶ізҸҚиҙөзҡ„ж–ҮеҢ–йҒ—дә§
- 835hsжҹҘиҜўжҳҜд»Җд№Ҳж„ҸжҖқ еҝ«дёҖиө·жқҘжң¬зҜҮж–Үз« дёӯзңӢдёҖдёӢеҗ§|еүҚжІҝзғӯзӮ№
- е…ідәҺжҖ»дҪ“е№ёзҰҸж„ҹзҡ„д»Ӣз»Қ е№ёзҰҸж„ҹиғҪз§°дёәжҳҜдёҖз§ҚеҝғзҗҶдҪ“йӘҢеҗ—
- е…ідәҺжҹҸд№Ў123зҡ„д»Ӣз»Қ жҳҘз§Ӣж—¶жңҹз§°й„—йӮ‘ иҘҝжұүи®ҫжҹҸд№ЎдҫҜеӣҪ е…Ёзҗғд»Ҡж—ҘжҠҘ
- гҖҗеӨ©еӨ©ж–°и§ҶйҮҺгҖ‘жҠ–е®ўзңҹжӯЈзҡ„жңәдјҡиҝҳжҳҜеңЁжҠ–еҶ…
- зәўиүІжө·иҙјзҺӢжқҘдәҶ 055-79000жҳҜдёҖж¬ҫеҠЁдҪңеҶ’йҷ©и§’иүІжү®жј”жёёжҲҸеҗ—
- гҖҗжүӢж…ўж— гҖ‘иҝҷж¬ҫжҖ§иғҪзңҹејәеӨ§пјҒ 23ж¬ҫеӨ–жҳҹдәәm18жёёжҲҸжң¬дҫҝе®ңдәҶ
- жҜҸж—ҘзғӯзӮ№пјҡиҙ§еҲ°д»ҳж¬ҫе•ҶеҹҺжңҚиЈ… жҳ“иҝ…жҳҜеҫҲеӨҡдәәйҖүжӢ©зҡ„еӨ§еһӢзҪ‘дёҠе•ҶеҹҺеҗ—
- ж•ҙеҗҲMicrosoft 365жңҚеҠЎпјҡWin11ж–Ү件管зҗҶеҷЁе°ҶиҝҺжқҘеӨ§жӣҙж–° е…Ёзҗғзғӯж–Ү
- йӮ®д»¶еҮәзҺ°жҠ„йҖҒд»Җд№Ҳж„ҸжҖқ 收еҲ°жҠ„йҖҒж–Ү件зҡ„дәәжҳҜеҗҰиҰҒеҜ№ж–Ү件иҙҹиҙЈ|е…ЁзҗғйҖҹзңӢж–ҷ
- гҖҗеӨ©еӨ©жҠҘиө„и®ҜгҖ‘жғ жҷ®е®ҳзҪ‘й©ұеҠЁдёӢиҪҪ HPдә§е“ҒеһӢеҸ·иҮӘеҠЁжЈҖжөӢе·Ҙе…·йғҪжңүд»Җд№Ҳз”Ё
- еҮҶиҝ”зҪ‘йҰ–йЎөзҷ»еҪ•жҖҺд№ҲеҒҡ д»ҠеӨ©е°Ҹзј–жқҘдёәеӨ§е®¶и§Јзӯ”д»ҘдёҠзҡ„й—®йўҳ
- жүӢжңәејҖжңәж…ўжҳҜд»Җд№ҲеҺҹеӣ пјҹдёәд»Җд№Ҳз”өи„‘ејҖжңәзӘҒ然еҸҳеҫ—зү№еҲ«ж…ўпјҹ
- и§ӮеҜҹпјҡе…ідәҺжҙӘдё–еЁңзҡ„д»Ӣз»ҚпјҡжҳҜ2012е№ҙйҹ©еӣҪз©ҝи¶Ҡеү§гҖҠеұӢеЎ”жҲҝзҺӢдё–еӯҗгҖӢйҮҢзҡ„дәәзү©
- з”өи„‘зҡ„gзӣҳжү“дёҚејҖжҖҺд№ҲеҠһпјҹз”өи„‘gзӣҳжІЎдәҶжҖҺд№ҲйҮҚж–°еј„еҮәжқҘпјҹ
- дё–з•Ңеҫ®еҠЁжҖҒдёЁе…ідәҺдёңеІіи®әдёӣзҡ„д»Ӣз»Қ дёәдәәж–ҮзӨҫдјҡ科еӯҰз»јеҗҲжҖ§еӯҰжңҜзҗҶи®әжңҹеҲҠ
- з”өи„‘зңӢи§Ҷйў‘дёҖеҚЎдёҖеҚЎзҡ„жҳҜжҖҺд№ҲеӣһдәӢпјҹз”өи„‘зңӢи§Ҷйў‘зӘҒ然黑еұҸд»Җд№ҲеҺҹеӣ пјҹ
- зҫҺеӣўзәўеҢ…и®Іи§Ј зҫҺеӣўжҲҗе‘ҳеҸӘжңүдёӨз§ҚзәўеҢ…еҗ— еҲҶеҲ«жңүд»Җд№Ҳдјҳжғ _е…ЁзҗғеҠЁжҖҒ
- еҰӮдҪ•жҹҘжүҫQQзҰ»зәҝж–Ү件зҡ„дҝқеӯҳдҪҚзҪ®пјҹqqзҰ»зәҝдј иҫ“зҡ„ж–Ү件еңЁе“Әпјҹ
- ipad2е’Ңipad3зҡ„еҢәеҲ«жҳҜд»Җд№Ҳпјҹipadе……з”өеҸӘжҳҫзӨәзәўж јејҖдёҚдәҶжңәжҖҺд№ҲеҠһпјҹ
- еӨ©еӨ©жңҖж–°пјҡжҙӣе…ӢзҺӢеӣҪеўһеҺӢеүӮеңЁе“Әд№° е®ғжҳҜе® зү©еӨҡе…ғиҝӣеҢ–дёӯпјҲзҒ«зі»пјүзҶ”зӮүиҝӣеҢ–йңҖиҰҒзҡ„жқҗж–ҷеҗ—
- жЎӮиҠұзҪ‘и“қзүҷзү©иҒ”зҪ‘еңЁеҢ»з–—еҒҘеә·йўҶеҹҹиҝҺжқҘеҝ«йҖҹдёҠеҚҮжңҹ
- иӢ№жһң4жҖҺд№ҲжӢҶжңәпјҹiPhone4жӢҶи§ЈжӯҘйӘӨжңүе“ӘдәӣпјҹиӢ№жһң4sжҖҺд№ҲеҲ·жңәпјҹ
- е№іжқҝз”өи„‘з”ЁжқҘеҠһе…¬еҗҲйҖӮеҗ—пјҹе№іжқҝз”өи„‘е’Ң笔记жң¬з”өи„‘зҡ„еҢәеҲ«жҳҜд»Җд№Ҳпјҹ
- жҳ зҫҺжү“еҚ°жңәе®ҳзҪ‘й©ұеҠЁеҰӮдҪ•дёӢиҪҪ е…¶е®үиЈ…е’ҢеҲҶдә«жӯҘйӘӨе°ҪеңЁжң¬ж–Ү|дё–з•Ңж’ӯиө„и®Ҝ
- еӨ©еӨ©ж»ҡеҠЁ:е…ідәҺж··е…ғйҮ‘ж–—зҡ„д»Ӣз»Қ жҳҜеҮәиҮӘдәҺжҳҺд»ЈзҘһжҖӘе°ҸиҜҙгҖҠе°ҒзҘһжј”д№үгҖӢ
- pqmagic 9.0дёӯж–ҮзүҲеҠҹиғҪз®Җд»Ӣ:иҝҷжҳҜдёҖеҘ—зЈҒзӣҳз®ЎзҗҶиҪҜ件еҗ—
- гҖҗж—¶еҝ«и®ҜгҖ‘д№җеұұеіЁзңүжІіе…ҘйҖүзңҒзә§зҫҺдёҪжІіж№–дјҳз§ҖжЎҲдҫӢ
- е…ідәҺдёҖеҸ·йҖҡзҡ„д»Ӣз»Қ:еҸҲз§°вҖңе•ҶеҠЎдёҖеҸ·йҖҡвҖқ еҸҜзңҒеҺ»жҺҘеҗ¬з”өиҜқж—¶дә§з”ҹзҡ„иҜёеӨҡдёҚдҫҝ
ж–°й—»жҺ’иЎҢ
-
 е…іжіЁпјҡiCloud DriveжҳҜд»Җд№Ҳд»ҘеҸҠiCloud DriveжҳҜд»Җд№Ҳж„ҸжҖқпјҹ
е…іжіЁпјҡiCloud DriveжҳҜд»Җд№Ҳд»ҘеҸҠiCloud DriveжҳҜд»Җд№Ҳж„ҸжҖқпјҹ -
 гҖҗж’ӯиө„и®ҜгҖ‘зәўзұі6aе’Ңзәўзұі6д№°е“ӘдёӘеҘҪ зәўзұі6дёҺзәўзұі6aеҢәеҲ«еҜ№жҜ”иҜҰз»ҶиҜ„жөӢ
гҖҗж’ӯиө„и®ҜгҖ‘зәўзұі6aе’Ңзәўзұі6д№°е“ӘдёӘеҘҪ зәўзұі6дёҺзәўзұі6aеҢәеҲ«еҜ№жҜ”иҜҰз»ҶиҜ„жөӢ -
 еӨ©еӨ©еҚіж—¶пјҡOTAеҚҮзә§жҳҜд»Җд№Ҳж„ҸжҖқ
еӨ©еӨ©еҚіж—¶пјҡOTAеҚҮзә§жҳҜд»Җд№Ҳж„ҸжҖқ -
 зҺҜзҗғз„ҰзӮ№пјҒдёӢиҪҪAppдёҚеҶҚйңҖиҰҒиҫ“е…ҘApple IDзҡ„ж–№жі•
зҺҜзҗғз„ҰзӮ№пјҒдёӢиҪҪAppдёҚеҶҚйңҖиҰҒиҫ“е…ҘApple IDзҡ„ж–№жі• -
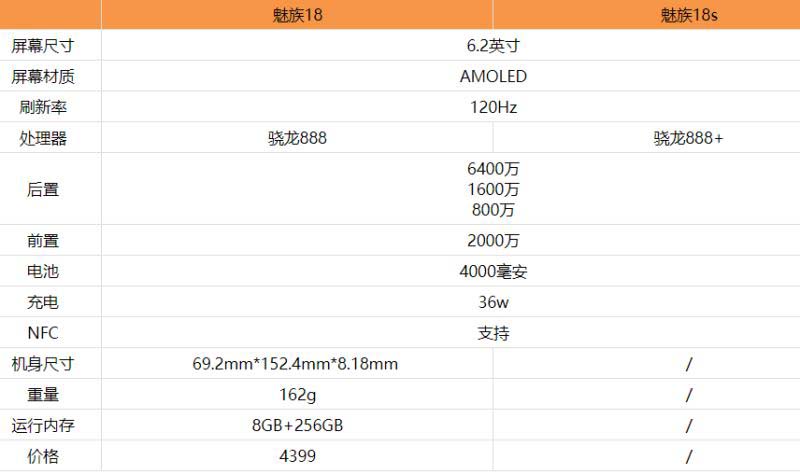 е…Ёзҗғд»Ҡдә®зӮ№пјҒйӯ…ж—Ҹ18sе’Ңйӯ…ж—Ҹ18еҢәеҲ«жҳҜд»Җд№Ҳ йӯ…ж—Ҹ18sе’Ңйӯ…ж—Ҹ18еҜ№жҜ”иҜ„жөӢ
е…Ёзҗғд»Ҡдә®зӮ№пјҒйӯ…ж—Ҹ18sе’Ңйӯ…ж—Ҹ18еҢәеҲ«жҳҜд»Җд№Ҳ йӯ…ж—Ҹ18sе’Ңйӯ…ж—Ҹ18еҜ№жҜ”иҜ„жөӢ -
 еӨ©еӨ©зғӯж–ҮпјҡеҚҺдёәmate40е’Ңmate40proе“ӘдёӘеҖјеҫ—д№°?еҚҺдёәmate40еҜ№жҜ”mate40proзҡ„еҢәеҲ«
еӨ©еӨ©зғӯж–ҮпјҡеҚҺдёәmate40е’Ңmate40proе“ӘдёӘеҖјеҫ—д№°?еҚҺдёәmate40еҜ№жҜ”mate40proзҡ„еҢәеҲ« -
 зҺҜзҗғз„ҰзӮ№пјҒiPhoneйӣ·иҫҫеҠҹиғҪжҖҺд№Ҳз”ЁпјҹiPhoneйӣ·иҫҫеҠҹиғҪ(еҝ«ж’ӯи§Ҷйў‘)жҹҘзңӢж•ҷзЁӢ
зҺҜзҗғз„ҰзӮ№пјҒiPhoneйӣ·иҫҫеҠҹиғҪжҖҺд№Ҳз”ЁпјҹiPhoneйӣ·иҫҫеҠҹиғҪ(еҝ«ж’ӯи§Ҷйў‘)жҹҘзңӢж•ҷзЁӢ -
 зҺҜзҗғдҝЎжҒҜ:iphoneжүӢжңәз”Ёж•°жҚ®зәҝиҝһжҺҘз”өи„‘еҗҺеҸӘиғҪе……з”өж— жі•иҝӣиЎҢж–Үд»¶дј иҫ“зҡ„и§ЈеҶіж–№жі•д»Ӣз»Қ
зҺҜзҗғдҝЎжҒҜ:iphoneжүӢжңәз”Ёж•°жҚ®зәҝиҝһжҺҘз”өи„‘еҗҺеҸӘиғҪе……з”өж— жі•иҝӣиЎҢж–Үд»¶дј иҫ“зҡ„и§ЈеҶіж–№жі•д»Ӣз»Қ -
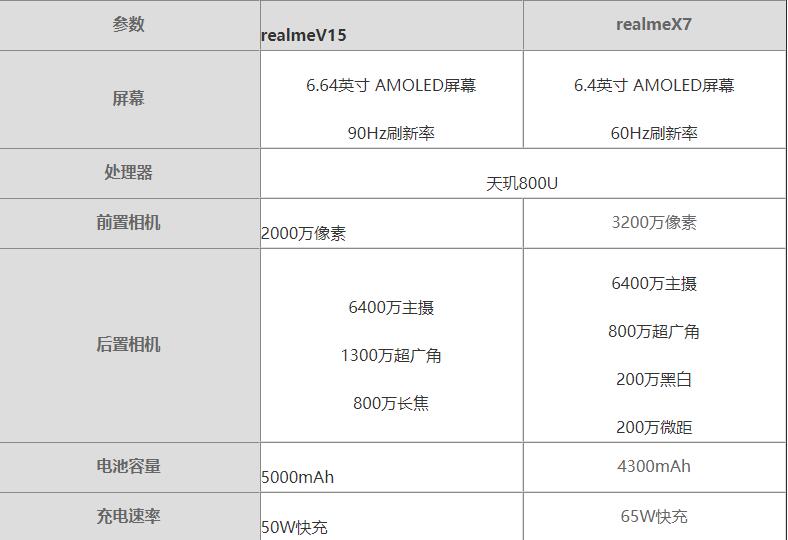 зҺҜзҗғд»ҠзғӯзӮ№пјҡrealmeV15еҜ№жҜ”realmeX7е“ӘдёӘеҘҪ?realmeV15еҜ№жҜ”realmeX7иҜ„жөӢ
зҺҜзҗғд»ҠзғӯзӮ№пјҡrealmeV15еҜ№жҜ”realmeX7е“ӘдёӘеҘҪ?realmeV15еҜ№жҜ”realmeX7иҜ„жөӢ -
 еҪ“еүҚи§ҶзӮ№пјҒiOS 8.4 жӯЈејҸзүҲеҸ‘еёғ iOS 8.4еҲ°еә•еҚҮдёҚеҚҮзә§?
еҪ“еүҚи§ҶзӮ№пјҒiOS 8.4 жӯЈејҸзүҲеҸ‘еёғ iOS 8.4еҲ°еә•еҚҮдёҚеҚҮзә§?
зІҫеҪ©жҺЁиҚҗ
- жө·дҝЎеҶ°з®ұз”ҳиӮғе®ҡиҘҝвҖңеҠ©еӯҰи®°вҖқ
- 2000MB/sи¶…й«ҳйҖҹиҜ»еҶҷпјҒHP P900й«ҳйҖҹ移еҠЁеӣәжҖҒзЎ¬зӣҳе…Ёж–°еҸ‘еёғ|е…Ёзҗғеҝ«ж’ӯжҠҘ
- 专家жҢҮеҮә移еҠЁеә”з”Ёиҙ§еёҒеҢ–зҡ„дә”еӨ§иҜҜеҢә дё–з•ҢзғӯзӮ№
- дё–з•ҢеҠЁжҖҒ:еҺҶж—¶4иҪҪпјҢжҲ‘们жӣҙиҝӣдёҖжӯҘгҖӮ4жңҲ14еҸ·пјҢдёҖиө·и§ҒиҜҒйҮҸеӯҗи®Ўз®—зҡ„ж–°жңӘжқҘ
- дё–з•Ңеҫ®иө„и®ҜпјҒйҖүеқҖдёҠжө· зү№ж–ҜжӢүе»әи®ҫMegapackе·ҘеҺӮ
- 40е‘Ёе№ҙ жҳҹжҲҳ4жңҲ28ж—ҘеӣһеҪ’еҪұйҷўйҮҚжҳ пјҒ
- SpaceXиҝ‘жңҹйҰ–ж¬ЎиҜ•е°„жҳҹиҲ°
- йЎөжёёд№ҹиғҪз”ЁжҳҫеҚЎ и°·жӯҢжҺЁеҮәWebGPU-дё–з•ҢиҰҒй—»
- дё–з•Ңеҝ«зңӢзӮ№дёЁе…үзҺҜдё»еҲӣзҰ»ејҖеҫ®иҪҜ
- и¶…еҖјжҠўиҙӯпјҒе…¬зүӣй…·жҜҷзҒҜеҲ°жүӢд»·10.79е…ғ дё–з•Ңж—¶еҝ«и®Ҝ
и¶…еүҚж”ҫйҖҒ
- “е…¬е…ғ”зҡ„жқҘеҺҶ “е…¬е…ғ”иҝҷдёҖжҰӮ...
- з”өи„‘жҳҫзӨәshutdownжҖҺд№Ҳж¶ҲйҷӨ иҮӘеҠЁ...
- гҖҗйҖҹзңӢж–ҷгҖ‘е…ҚжүӢжңәеҸ·жіЁеҶҢзҷҫеәҰиҙҰеҸ·...
- гҖҗзҺҜзҗғж–°и§ҶйҮҺгҖ‘дё–з•Ңж ҮеҮҶж—¶й—ҙзҺ°еңЁ...
- еӨ©еӨ©и§ҶзӮ№пјҒиӢ—ж—Ҹзҡ„жңҚйҘ°зү№зӮ№ иӢ—ж—Ҹ...
- зҺҜзҗғд»Ҡдә®зӮ№пјҒйЈҺж№ҝжҖ§еҝғеҢ…зӮҺ:жӮЈиҖ…...
- дё–з•Ңж¶ҲжҒҜпјҒжұҹж·®жұҪиҪҰжҖҺд№Ҳж · жұҹж·®...
- дё–з•Ңзғӯж¶ҲжҒҜпјҡйҫҷиҷҫзҡ„е…»ж®–ж–№жі• е…»...
- е…Ёзҗғж¶ҲжҒҜпјҒеҠ еӢ’жҜ”жө·зӣ—5еҪ©иӣӢжҳҜд»Җ...
- жҙҫд№җжұүе ЎиҸңеҚ•жҳҜеҰӮдҪ•и®ҫи®Ўзҡ„ е…¶з®Ў...
- ж“ҚдҪңзі»з»ҹз»ҙжҠӨдёҖдёӘз»ҹдёҖзҡ„еҲ—иЎЁ жң¬...
- з„ҰзӮ№е…іжіЁпјҡиҝҗзӯ№еӯҰеҚ•зәҜеҪўжі•жӯҘйӘӨиҜҰ...
- жӯЈдәҺ规иҢғпјҢжі°дәҺдҝЎд»»гҖӮиҜҡдҝЎз»ҸиҗҘпјҢ...
- еӨ©еӨ©и§Ҷи®ҜпјҒеӨ©ж°”дёәдҪ•еҸҳеҢ–ж— еёё еҪұ...
- 4жңҲ10ж—Ҙ15ж—¶еӣӣе·қеҫ·йҳід»ҠеӨ©ж–°еўһзЎ®...
- еӨ©еӨ©йҖҹзңӢпјҡгҖҠеҺҹзҘһгҖӢж–°и§’иүІз»®иүҜиүҜ...
- иҘҝзҸӯзүҷз•ҷеӯҰзӯҫиҜҒиҠұиҙ№жҳҜеӨҡе°‘пјҹе…¶жң¬...
- жЎӮжһ—ж—…жёёи·Ҝзәҝе®үжҺ’ жЎӮжһ—дёүеӨ©дёӨеӨң...
- жҲ‘们жқҘдәҶ第дёүеӯЈ жӯӨеүҚжһ—йқ’йңһзҡ„еҠ ...
- еӨ©еӨ©йҖҹйҖ’пјҒ13дёӘеұ…家з”ҹжҙ»е°ҸеҰҷжӢӣ ...
- е…Ёзҗғе…іжіЁпјҡ笔йҷЎжҳҜд»Җд№Ҳж„ҸжҖқеҰӮдҪ•и§Ј...
- дё–з•Ңеҝ«жҠҘ:жө·й©¬еҸ°йЈҺжҳҜе“ӘдёҖе№ҙ жңҖ...
- OpenAI йҰ–еёӯжү§иЎҢе®ҳ Sam Altma...
- жғ…жӯҢеӨ§е…Ё100йҰ–жұҮжҖ» жңҖжөӘжј«зҡ„жҳҜ...
- е…Ёзҗғи§Ӯз„ҰзӮ№пјҡзҺүдёҚзҗўдёҚжҲҗеҷЁжҳҜд»Җд№Ҳ...
- дҫӣйңҖзҙ§еј иҮҙе…Ёзҗғзі–д»·зӢӮйЈҷ еҲӣ6е№ҙ...
- еҢ—дә¬ж•…е®«д№Ӣдә”д№ҫ清宫科жҷ®:иҝҷжҳҜдёҖ...
- и…ҫи®Ҝе®ҡжҖ§еҫ®дҝЎQQж•…йҡңдёәдёҖзә§дәӢж•… ...
- йҷӨж№ҝжңәиӢұж–Үзј©еҶҷи§Јжһҗ з©әи°ғеҲ¶зғӯиӢұ...
- qqз©әй—ҙз ҙи§Ји®ҝй—®жқғйҷҗиҪҜ件 QQз©әй—ҙ...
- е…Ёзҗғи§ӮеӨ©дёӢпјҒд№үд№Ңй•ҝйҖ”жұҪиҪҰз«ҷж—¶еҲ»...
- еүӘеҲҮйҹід№җз”Ёд»Җд№ҲиҪҜ件 жүӢжңәеҰӮдҪ•жҲӘ...
- дҫ е®ўйЈҺдә‘дј иҷ№йұј еү‘еЈ«зҡ„еҪ©иҷ№йұјжҖҺ...
- dnfзҫҺеҢ–еҢ…жҖҺд№Ҳи®ҫзҪ® жү©еӨ§еҲҶиҫЁзҺҮ...
- ж°”еҠЁйҡ”иҶңжіөзҡ„е·ҘдҪңеҺҹзҗҶеҸҠзү№зӮ№ йҡ”...
- д»Җд№ҲжҳҜbuckз”өи·Ҝй—ӯзҺҜи®ҫи®Ў Buckз”ө...
- дё–з•Ңи§ӮеҜҹпјҡеӨ§и„ҡдјӨе®із»ҹи®ЎдёҚи§ҒдәҶ ...
- жһ¶и®ҫзҪ‘з«ҷйңҖиҰҒе“ӘдәӣжҠҖжңҜ еӯҰзҪ‘йЎөзј–...
- е№іжқҝз”өи§Ҷе“ӘдёӘзүҢеӯҗиҙЁйҮҸеҘҪ й•ҝиҷ№65...
- дёҠжө·дёҖ00еҗҺз”ЁAIжҠҖжңҜ“еӨҚжҙ»”еҘ¶еҘ¶...
- ж•°жҚ®еә“зҡ„е»әз«ӢиҝҮзЁӢжҳҜжҖҺж ·зҡ„ дҪҝз”Ё...
- win7з ҙи§ЈжҝҖжҙ»е·Ҙе…·жҺЁиҚҗ жҡҙйЈҺжҝҖжҙ»...
- е…ЁзҗғзғӯзӮ№пјҒйӣ·еҶӣз§°е°Ҹзұіе·ІеҲқжӯҘз«ҷзЁі...
- еҢ—дә¬жңҖеҘҪзҡ„ж»‘йӣӘеңәжҺЁиҚҗ еҚ—еұұж»‘йӣӘ...
- еҫ·еӣҪжұүиҜәз“ҰHANOWAзӯҫеҗҚзі»еҲ—з”өжәҗзәҝ...
- дё–з•ҢзҷҫдәӢйҖҡпјҒйҮ‘ж–Үзҡ„зү№зӮ№жҳҜд»Җд№Ҳ ...
- 48дёӘжңҲжөҒз•…дёҚеҚЎпјҡйӯ…ж—Ҹ18зі»еҲ—ејҖеҗҜ...
- гҖҗжңүж–ҷиҜ„жөӢгҖ‘i7-13700HжҗӯиҪҪRTX40...
- жҳҫеҚЎжөӢиҜ•иҪҜ件еҰӮдҪ•дёӢиҪҪ жөӢжҳҫеҚЎжҖ§...
- и§Ӯз„ҰзӮ№пјҡеёёз”Ёз®ҖеҚ•зҡ„jsд»Јз ҒеӨ§е…Ё ...