еҚ•зәҜеҪўжі•з®ҖеҚ•дҫӢйўҳиҜҰи§Ј и®°дҪҸзәҝжҖ§и§„еҲ’жҳҜиҝҗзӯ№еӯҰзҡ„дёҖдёӘйҮҚиҰҒеҲҶж”Ҝ|еӨ©еӨ©еҝ«зңӢзӮ№
е…ідәҺиҝҗзӯ№еӯҰеҚ•зәҜеҪўжі•пјҲеҚ•зәҜеҪўжі•з®ҖеҚ•дҫӢйўҳиҜҰи§Јпјү зҡ„зҹҘиҜҶеӨ§е®¶дәҶи§Јеҗ—пјҹд»ҘдёӢе°ұжҳҜе°Ҹзј–ж•ҙзҗҶзҡ„е…ідәҺиҝҗзӯ№еӯҰеҚ•зәҜеҪўжі•пјҲеҚ•зәҜеҪўжі•з®ҖеҚ•дҫӢйўҳиҜҰи§Јпјү зҡ„д»Ӣз»ҚпјҢеёҢжңӣеҸҜд»Ҙз»ҷеҲ°еӨ§е®¶дёҖдәӣеҸӮиҖғпјҢдёҖиө·жқҘдәҶи§ЈдёӢеҗ§пјҒ
иҝҗзӯ№еӯҰзҡ„еҚ•зәҜеҪўжі•(еҚ•зәҜеҪўжі•з®ҖеҚ•дҫӢеӯҗзҡ„иҜҰз»Ҷи§ЈйҮҠ)
 (иө„ж–ҷеӣҫ)
(иө„ж–ҷеӣҫ)
иҙҰеҸ·жҳҜеҚҺдёәдә‘ејҖеҸ‘иҖ…зӨҫеҢәзҡ„е®ҳж–№иҝҗиҗҘиҙҰеҸ·пјҢжҸҗдҫӣе…Ёйқўж·ұе…Ҙзҡ„дә‘и®Ўз®—еүҚжҷҜеҲҶжһҗпјҢдё°еҜҢзҡ„жҠҖжңҜе№Іиҙ§гҖҒзЁӢеәҸж ·жң¬пјҢеҲҶдә«еҚҺдёәдә‘еүҚжІҝиө„и®ҜеҠЁжҖҒгҖӮ
жң¬ж–ҮеҲҶдә«иҮӘеҚҺдёәдә‘зӨҫеҢәзҡ„еҜ№еҒ¶зҗҶи®әе’ҢеҜ№еҒ¶з®ҖеҚ•е®ҡеҫӢгҖӮеҺҹдҪңиҖ…жҳҜдә•еҶҲеұұ_йҳіжҳҘгҖӮ
зәҝжҖ§и§„еҲ’жҳҜиҝҗзӯ№еӯҰзҡ„дёҖдёӘйҮҚиҰҒеҲҶж”ҜпјҢз ”з©¶ж—©пјҢеҸ‘еұ•еҝ«пјҢеә”з”Ёе№ҝпјҢж–№жі•жҲҗзҶҹгҖӮе®ғжҳҜдёҖз§Қиҫ…еҠ©дәә们иҝӣиЎҢ科еӯҰз®ЎзҗҶзҡ„ж•°еӯҰж–№жі•гҖӮеҜ№еҒ¶зҗҶи®әжҳҜз ”з©¶зәҝжҖ§и§„еҲ’дёӯеҺҹе§Ӣй—®йўҳе’ҢеҜ№еҒ¶й—®йўҳд№Ӣй—ҙе…ізі»зҡ„зҗҶи®әгҖӮ
1.жҸҗеҮәеҜ№еҒ¶й—®йўҳгҖӮ
дәҢе…ғжҖ§жҳҜеҗҢдёҖй—®йўҳд»ҺдёӨдёӘдёҚеҗҢи§’еәҰзҡ„иЎЁиҫҫгҖӮдҫӢеҰӮпјҢвҖңзҹ©еҪўйқўз§ҜдёҺе‘Ёй•ҝзҡ„е…ізі»вҖқжңүд»ҘдёӢдёӨз§ҚиЎЁиҫҫејҸ:
жңүдёҖе®ҡе‘Ёй•ҝдё”йқўз§ҜжӣҙеӨ§зҡ„й•ҝж–№еҪўжҳҜжӯЈж–№еҪўпјӣ
жңүдёҖе®ҡйқўз§Ҝдё”е‘Ёй•ҝжңҖзҹӯзҡ„зҹ©еҪўжҳҜжӯЈж–№еҪўгҖӮ
жҜ”еҰӮз”ҹдә§и®ЎеҲ’зҡ„й—®йўҳпјҢеҰӮеӣҫ1жүҖзӨәпјҢдёҖдёӘе·ҘеҺӮиҰҒз”ҹдә§дёӨз§Қдә§е“ҒIе’ҢIIпјҢеҺҹж–ҷеҲҶеҲ«жҳҜAе’ҢBпјҢеҜ№жҖ»зҡ„з”ҹдә§и®ҫеӨҮд№ҹжңүйҷҗеҲ¶гҖӮ
然еҗҺпјҢеҲҶеҲ«з”ҹдә§еӨҡ少件дә§е“ҒIе’ҢIIпјҢдҪҝз”ҹдә§зҡ„еҲ©зӣҠжӣҙеӨ§еҢ–гҖӮжҳҫ然пјҢд»ҺеҚ–ж–№зҡ„и§’еәҰжқҘзңӢпјҢеҲ©з”ЁзәҝжҖ§и§„еҲ’пјҢеҸҜд»Ҙеҫ—еҲ°дјҳеҢ–жЁЎеһӢM1:
е…¶дёӯx1е’Ңx2еҲҶеҲ«жҳҜи®ЎеҲ’дә§е“ҒIе’ҢIIзҡ„ж•°йҮҸгҖӮжҚўдёӘи§’еәҰжқҘиҜҙпјҢд»Һд№°ж–№зҡ„и§’еәҰжқҘиҜҙпјҢдёҚд№°дә§е“ҒпјҢеҸҜд»ҘзӣҙжҺҘд№°еҺҹжқҗж–ҷгҖӮд»ҺеҲ©ж¶Ұзҡ„и§’еәҰеҮәеҸ‘пјҢеҒҮи®ҫжҜҸз§ҚеҺҹж–ҷзҡ„д»·ж јдёҺy1гҖҒy2гҖҒy3зҡ„д»·ж јдёҚеҗҢпјҢд№°ж–№жғід№°жҲҗжң¬жӣҙдҪҺзҡ„пјҢдәҺжҳҜжңүд»ҘдёӢдјҳеҢ–жЁЎеһӢM2:
д»ҘдёҠжҳҜиҜҙжҳҺеҜ№еҒ¶й—®йўҳзҡ„дёӨдёӘдҫӢеӯҗгҖӮеҺҹе§Ӣй—®йўҳе’ҢеҜ№еҒ¶й—®йўҳзҡ„еҜ№еә”иЎЁзӣҙжҺҘеңЁдёӢйқўз»ҷеҮә:
иҝҷз§ҚеҜ№еә”е…ізі»еҸҜд»Ҙд»ҺжӢүж јжң—ж—ҘеҜ№еҒ¶дёӯжҺЁеҜјеҮәжқҘпјҢиҝҷйҮҢдёҚе…·дҪ“д»Ӣз»ҚгҖӮж„ҹе…ҙи¶Јзҡ„еҗҢеӯҰеҸҜд»ҘеҸӮиҖғhttps://www.zhihu.com/question/58584814.
2.LPж ҮеҮҶй—®йўҳзҡ„еҜ№еҒ¶й—®йўҳ
ж ҮеҮҶLPй—®йўҳ:
еҸҢйҮҚй—®йўҳ:
еҜ№еҺҹй—®йўҳе’ҢеҜ№еҒ¶й—®йўҳзҡ„и§Јд№Ӣй—ҙзҡ„е…ізі»еҒҡдёҖдәӣз®ҖеҚ•зҡ„жҺЁеҜј:
е…¶дёӯxBе’ҢxNеҲҶеҲ«еҜ№еә”еҹәжң¬еҸҳйҮҸе’Ңйқһеҹәжң¬еҸҳйҮҸпјҢBе’ҢNжҳҜеҜ№еә”еҹәжң¬еҸҳйҮҸе’Ңйқһеҹәжң¬еҸҳйҮҸзҡ„зҹ©йҳөпјҢcBе’ҢcNеҜ№еә”жҲҗжң¬зі»ж•°гҖӮд»ҺдёҠйқўзҡ„жҺЁеҜјеҸҜд»ҘзңӢеҮәпјҢеҜ№еҒ¶й—®йўҳзҡ„и§ЈдёҺеҺҹй—®йўҳзҡ„жөӢиҜ•ж•°д№Ӣй—ҙеӯҳеңЁеҜ№еә”е…ізі»пјҢиҝҷеҜ№дәҺзҗҶи§ЈеҜ№еҒ¶еҚ•зәҜеҪўжі•жҳҜйқһеёёйҮҚиҰҒзҡ„гҖӮ
3.еҜ№еҒ¶й—®йўҳзҡ„жҖ§иҙЁ
3.1еҜ№з§°жҖ§
3.2ејұдәҢе…ғжҖ§
ејұеҜ№еҒ¶иЎЁзӨәеҸӘиҰҒжүҫеҲ°еҺҹй—®йўҳе’ҢеҜ№еҒ¶й—®йўҳзҡ„дёҖдёӘеҸҜиЎҢи§ЈпјҢе°ұеҸҜд»ҘзЎ®е®ҡеҪјжӯӨзҡ„дёҠдёӢз•ҢгҖӮд»ҺејұеҜ№еҒ¶дёӯеҸҜд»Ҙеҫ—еҮәдёӨдёӘйҮҚиҰҒзҡ„жҺЁи®ә:
3.3ејәдәҢе…ғжҖ§
3.4жӣҙдҪіжқЎд»¶
4.еҸҢйҮҚз®ҖеҚ•ж–№жі•
йҰ–е…Ҳд»ҺеӨ§зҡ„жҰӮеҝөдёҠпјҢзҗҶи§ЈеҺҹеҚ•зәҜеҪўжі•е’ҢеҜ№еҒ¶еҚ•зәҜеҪўжі•:
е…¶ж¬ЎпјҢжҺЁеҜјдәҶеҜ№еҒ¶еҚ•зәҜеҪўжі•гҖӮе…¶е®һеҜ№еҒ¶еҚ•зәҜеҪўжі•е’ҢеҚ•зәҜеҪўжі•зҡ„дё»иҰҒеҢәеҲ«еңЁдәҺиҝӣеҹәе’ҢеҮәеҹәзҡ„зӯ–з•ҘдёҚеҗҢгҖӮиҝҷйҮҢиҜҰз»Ҷд»Ӣз»ҚдәҶеҜ№еҒ¶еҚ•зәҜеҪўжі•иҝӣеҹәзӯ–з•Ҙе’ҢйҖҖеҹәзӯ–з•Ҙзҡ„жҺЁеҜјгҖӮйңҖиҰҒејәи°ғзҡ„жҳҜпјҢеҜ№еҒ¶еҚ•зәҜеҪўжі•жҺЁеҜјзҡ„еүҚжҸҗжҳҜеҲқе§Ӣи§Јж»Ўи¶іеҜ№еҒ¶еҸҜиЎҢ(еҺҹй—®йўҳзҡ„жөӢиҜ•ж•°е…ЁйғЁеӨ§дәҺ0)гҖӮ
жңҖеҗҺпјҢз»ҷеҮәдәҶеҜ№еҒ¶еҚ•зәҜеҪўжі•зҡ„е…·дҪ“жӯҘйӘӨ:
\- вҖңиҮӘеңЁи§Ҷеҗ¬пјҢд»Ҙи§ӮеҝғеўғвҖқдёңиҠқз”өи§Ҷ2023ж–°е“ҒйңҮж’јеҸ‘еёғ|д»Ҡж—ҘзІҫйҖү
- зҺҜзҗғеҠЁжҖҒ:еңЁиөЈзҘһйӯ”пјҹгҖҠForspokenгҖӢжҺЁеҮәе…Қиҙ№зҫҺз”ІDLC
- еҝ«зңӢзӮ№дёЁ6жңҲеҒңжӯўж”ҜжҢҒпјҒеҫ®иҪҜеӮ¬Win10 21H2з”ЁжҲ·еҚҮзә§Win11
- дё–з•Ңи§Ҷи®ҜпјҒвҖңйІңзҶҹйӯ”зӣ’вҖқжңүеӨҡд№Ҳзҡ„зҘһеҘҮпјҹе®№еЈ°еҶ°з®ұеҸҢеҮҖж— иҫ№з•Ң506е‘ҠиҜүдҪ зӯ”жЎҲ
- е…Ёзҗғе…іжіЁпјҡ4жңҲ07ж—Ҙ14ж—¶й»‘йҫҷжұҹзүЎдё№жұҹжңҖж–°з–«жғ…йҳІжҺ§дҝЎжҒҜ 4жңҲ07ж—Ҙ14ж—¶й»‘йҫҷжұҹзүЎдё№жұҹд»ҠеӨ©еҮәеӨҡе°‘йҳіжҖ§
- еҪ“еүҚиө„и®Ҝ!иҒҡз„ҰдёҡеҠЎж•°жҚ®е®үе…Ёе…ЁжөҒзЁӢпјҢж–°еҚҺдёүеӨҜе®һж•°еӯ—йҮ‘иһҚе®үе…Ёеә•еә§
- дј з»ҹиЎҘе…үиҝҺжқҘвҖңеҠІж•ҢвҖқпјҒжІӘе…үй«ҳз«Ҝзӣҙж’ӯзҡ„зҗҶжғід№ӢйҖү|дё–з•Ңеҝ«зңӢзӮ№
- е°Ҹзұі13 UltraеӨ–и§Ӯжӣқе…үпјҡзҲҶж–ҷе…ЁдёӯпјҒ-е…Ёзҗғж–°ж¶ҲжҒҜ
- е…Ёзҗғзҹӯи®ҜпјҒе·Ҙиө„6000йқўиҜ•6иҪ®еҪ“дәӢдәәеҸ‘еЈ°пјҡжІЎиў«еҪ•з”Ё еҸҜиғҪд»Ӣж„ҸжҲ‘е№ҙйҫ„еӨ§
- йҳҝйҮҢдә‘еӨ§жЁЎеһӢз ”з©¶жҲҗжһңдә®зӣё вҖңйҖҡд№үеҚғй—®вҖқејҖеҗҜдјҒдёҡйӮҖжөӢ_дё–з•ҢжҠҘиө„и®Ҝ
- еӨ©еӨ©и§Ӯз„ҰзӮ№пјҡжқӯе·һйҳҝйҮҢе·ҙе·ҙз”ұ122дәҝеҮҸиө„иҮі1дәҝ е®ҳж–№еӣһеә”пјҡзі»е…¬еҸёжӯЈеёёе·Ҙе•Ҷзҷ»и®°еҸҳжӣҙ
- е…·дҝҠжҷ”иҜҙзӯүдәҶеӨ§SдәҢеҚҒе№ҙ дҪ иҜҙжҲ‘дҝЎдёҚдҝЎзҡ„еҠЁжҖҒеӣҫ_зғӯзӮ№иҒҡз„Ұ
- дәҡ马йҖҠеӨ§йқўз§ҜиЈҒе‘ҳжіўеҸҠжёёжҲҸйғЁй—Ё иҝ‘100еҗҚе‘ҳе·Ҙе°ҶеҸ—еҪұе“Қ
- е…¬еҸёи®ҫж—©йёҹжҷҡйёҹеҘ–жҝҖеҠұе‘ҳе·Ҙж—©еҲ°жҷҡйҖҖ жңүдәәдҝ©жңҲиөҡ7000
- 4жңҲ07ж—Ҙ13ж—¶е№ҝдёңиҢӮеҗҚз–«жғ…йҳІжҺ§жғ…еҶө 4жңҲ07ж—Ҙ13ж—¶е№ҝдёңиҢӮеҗҚз–«жғ…жңҖж–°йҖҡзҹҘ|жҜҸж—Ҙеҝ«ж’ӯ
- е°Ҹзұі13 UltraжҗӯиҪҪеҫ•еҚЎSummicronй•ңеӨҙ иҝҗз”ЁеҲ’ж—¶д»ЈжҠҖжңҜ
- иғҶеҲҮйҷӨеҗҺжңүд»Җд№ҲеҪұе“Қ
- жҜ”дәҡиҝӘзҷҫдёҮзә§зәҜз”өи¶…и·‘пјҒд»°жңӣU9зЎ®е®ҡеҸӮеҠ дёҠжө·иҪҰеұ•пјҡеҠ йҖҹ2з§’зә§|дё–з•ҢзғӯжҺЁиҚҗ
- зңӢзӮ№пјҡгҖҗжүӢж…ўж— гҖ‘еҸӘиҰҒ3299е…ғпјҒе…ҘжүӢThinkPad X13й”җйҫҷ5й«ҳжҖ§иғҪиҪ»и–„жң¬
- 4жңҲ07ж—Ҙ12ж—¶жөҷжұҹжқӯе·һжңҖж–°з–«жғ…йҳІжҺ§дҝЎжҒҜ 4жңҲ07ж—Ҙ12ж—¶жөҷжұҹжқӯе·һд»ҠеӨ©еҮәеӨҡе°‘йҳіжҖ§ еӨ©еӨ©зғӯи®®
- гҖҠи¶…зә§й©¬еҠӣ欧гҖӢеӨ§зҲҶпјҒеӨҡеӣҪз ҙзәӘеҪ• д»Ҡе№ҙжңҖдҪійҰ–ж—ҘжҲҗз»©-зҺҜзҗғиҒҡзңӢзӮ№
- д»Ҡж—ҘжҺЁиҚҗпјҡгҖҠNBA2K23гҖӢ49е…ғ|гҖҠжңҖеҗҺзҡ„зҜқзҒ«гҖӢ10е…ғ
- жҜҸж—Ҙеҝ«и®Ҝ!зҙ йҘәеӯҗйҰ…еҒҡжі•еӨ§е…ЁиҸңи°ұзӘҚй—Ё_зҙ йҘәеӯҗйҰ…еҒҡжі•
- е…Ёзҗғи®ҜжҒҜпјҡй•ҝиҫҫ9е№ҙз»ҙжҠӨиө°еҗ‘е°ҪеӨҙпјҒгҖҠжҡ—й»‘з ҙеқҸзҘһ3гҖӢе®ЈеёғиөӣеӯЈеҚіе°ҶеҒңжӣҙ
- 6жңҲеҒңжӯўж”ҜжҢҒпјҒеҫ®иҪҜеҶҚж¬Ўж•ҰдҝғWin10 21H2з”ЁжҲ·еҚҮзә§Win11
- еҪ“еүҚжҠҘйҒ“:и¶…й•ҝз»ӯиҲӘпјҒиҚЈиҖҖж–°ж¬ҫMagicBook 14зі»еҲ—е®ҡжЎЈпјҡд»ЈеҸ·вҖңдёүеҸүжҲҹвҖқ
- гҖҗе…Ёзҗғж–°и§ҶйҮҺгҖ‘GoogleжҺЁеҮәWebGPUжҠҖжңҜ з”ЁдәҺеңЁжөҸи§ҲеҷЁдёӯиҝӣиЎҢдёӢдёҖд»ЈжёёжҲҸ
- еҸҲж¶үе«ҢйҖ и°ЈпјҒChatGPTзј–йҖ жі•еӯҰж•ҷжҺҲжҖ§йӘҡжү°
- дә¬дёңз”өи„‘ж•°з Ғ7856е…ғеҚіеҸҜе…ҘжүӢе°јеә·зӣёжңәеҸҳиә«иөҸиҠұVlogеҚҡдё»дёҚз”Ёзӯү зҺҜзҗғеҫ®еӨҙжқЎ
- жҠ–йҹідёҺи…ҫи®Ҝи§Ҷйў‘иҫҫжҲҗеҗҲдҪң дәҢеҲӣдҪңиҖ…ж”ҫеҝғдәҶ
- е°Ҹзәўд№ҰиҝӣйҖҖдёӨйҡҫпјҢз•ҷз»ҷжҜӣж–Үи¶…зҡ„ж—¶й—ҙдёҚеӨҡдәҶ-еүҚжІҝзғӯзӮ№
- AIGCжҠҖжңҜе‘ЁжҠҘпҪңChatDoctorпјҡе“ӘйҮҢдёҚиҲ’жңҚпјӣHuggingGPTпјҡиҝһжҺҘеӨ§жЁЎеһӢе’ҢжңәеҷЁеӯҰд№ зӨҫеҢәпјӣChatGPTзңҹзҡ„йІҒжЈ’еҗ—пјҹ_жҜҸж—Ҙж—¶и®Ҝ
- зҺҜзҗғеҚіж—¶пјҡvivo X Fold2еұҸ幕еӨҡеӨ§пјҹеұҸ幕е°әеҜёеҲ·ж–°зҺҮеӨ§е°ҸеҸӮж•°жӣқе…ү
- ROG 7 ProжёёжҲҸжүӢжңәеӨ–и§Ӯжӣқе…үпјҡз”өз«һе°ҸеұҸ+жЁӘеҗ‘дёүж‘„
- зҺҜзҗғзғӯи®®:дёӯеӣҪе№ҝз”ө5Gе…Ёйқўж”ҜжҢҒiPhone е°ҶжҺЁеҮәеҗҲзәҰеҘ—йӨҗ
- XboxгҖҠеҺҹеӯҗд№ӢеҝғгҖӢйҷҗе®ҡдё»жңәе…¬ејҖпјҡеҶ°з®ұйӯ…йӯ”дјҙиә«иҫ№
- еҚҮ13д»Јй…·зқҝ4399е…ғиө· еҸҜйҖү 2.5KеұҸ жғ жҷ®жҲҳ66е…ӯд»Јй…·зқҝзүҲиҜ йҮҠе•ҶеҠЎжң¬жҖ§иғҪж–°ж ҮжқҶ
- йӯ…ж—Ҹ20/20 ProжҺЁйҖҒзі»з»ҹжӣҙж–° ж–°еўһеӣҫзүҮиҜҶеҸ–дё»дҪ“зӯүеҠҹиғҪ
- 4жңҲ07ж—Ҙ11ж—¶еұұиҘҝеҗ•жўҒз–«жғ…жңҖж–°йҖҡжҠҘд»ҠеӨ© 4жңҲ07ж—Ҙ11ж—¶еұұиҘҝеҗ•жўҒд»Ҡж—Ҙж–°еўһжҙ»еҠЁиҪЁиҝ№жңүеҗ—
- зҺҜзҗғи§ӮзӮ№пјҡ4жңҲ07ж—Ҙ11ж—¶жІіеҚ—еҚ—йҳіз–«жғ…жңҖж–°ж¶ҲжҒҜ 4жңҲ07ж—Ҙ11ж—¶жІіеҚ—еҚ—йҳід»Ҡж—ҘзЎ®иҜҠдәәж•°
- дё–з•Ңеҝ«зңӢзӮ№дёЁзү№ж–ҜжӢүQ1еңЁеҫ·еӣҪй”ҖйҮҸеҗҢжҜ”еӨ§еўһ43% дҪҶ3жңҲд»ҪеҗҢжҜ”д»…еўһй•ҝ8.2%
- гҖҗе…Ёзҗғж–°иҰҒй—»гҖ‘гҖҗжүӢж…ўж— гҖ‘и–…зҫҠжҜӣ 1еҲҶй’ұеҢ…йӮ®0.5зұіCAT6еҚғе…ҶзҪ‘зәҝ
- гҖҗжүӢж…ўж— гҖ‘жҖ§д»·жҜ”еӨӘж— ж•ҢпјҒ6167е…ғе…ҘзҘһиҲҹжҲҳзҘһZ8笔记жң¬з”өи„‘ еӨ©еӨ©дҝЎжҒҜ
- жңҖж–°пјҡгҖҗжүӢж…ўж— гҖ‘жһӯйІё8GB DDR3笔记жң¬еҶ…еӯҳжқЎ1600MHzд»…34.9е…ғ
- зӘғиҙјжү“жҙһиҝӣиӢ№жһңй—Ёеә—зӣ—иө°iPhoneгҖҒiPadзӯүе•Ҷе“Ғ жҖ»д»·еҖјзәҰ50дёҮзҫҺе…ғ-дё–з•ҢзҷҫдәӢйҖҡ
- е…Ёзҗғеҫ®еҠЁжҖҒдёЁиҪ»зӣҗAppеҒңз”Ё е®ЈеёғжңҚеҠЎеҷЁе°Ҷж°ёд№…е…ій—ӯ
- 马ж–Ҝе…ӢеӨҚеҺҹжҺЁзү№йҰ–йЎөLogo жҚўеӣһи“қиүІйёҪеӯҗ
- зҺӢеӯҗж–ҮеҶҚзҷ»жқӮеҝ—е°ҒйқўпјҢзҪ®иә«дёӣжһ—зҫҺеҰӮзІҫзҒөпјҢиЎЁжҖҒеҚ•иә«еҗҺжӣҙжңүйӯ…еҠӣ
- ж‘©жүҳзҪ—жӢүk2зҡ„иҜ„д»·пјҡеңЁеӨ–и§ӮдёҠ延з»ӯдәҶж‘©жүҳзҪ—жӢүжөҒиЎҢзҡ„иҪ»гҖҒи–„гҖҒзӘ„йЈҺж ј
- дёӯеӣҪеҹҺй•ҮдәәеҸЈе·ІзӘҒз ҙ9дәҝ 10е№ҙй—ҙеўһй•ҝи¶…2.3дәҝ ж•°жҚ®е–ңдәә_зҺҜзҗғи§ӮйҖҹи®Ҝ
- дё–з•ҢиҰҒй—»пјҡгҖҠе®Ҳжңӣе…Ҳй”ӢпјҡеҪ’жқҘгҖӢејҖеҸ‘иҖ…д»Ӣз»Қпјҡж–°иӢұйӣ„вҖңз»Үе‘ҪвҖқ
- зҺӢиҖ…иҚЈиҖҖs22жӣҙж–°дёҚдәҶ еҠ иҪҪиҝӣеәҰжқЎдјҡеҚЎеңЁ45%иҜҘжҖҺд№Ҳи§ЈеҶі
- htc vivaжүӢжңәпјҡжӢҘжңү2.8иӢұеҜё65000иүІTFTи§Ұж‘ёеұҸ иҺ·еҫ—дәҶдј—еӨҡеҘҪиҜ„
- еӨ©еӨ©жңҖиө„и®ҜдёЁ4жңҲ07ж—Ҙ10ж—¶ж№–еҚ—еЁ„еә•жңҖж–°з–«жғ…йҳІжҺ§дҝЎжҒҜ 4жңҲ07ж—Ҙ10ж—¶ж№–еҚ—еЁ„еә•д»ҠеӨ©еҮәеӨҡе°‘йҳіжҖ§
- е…ідәҺжёёжҲҸдёӯзІҫзҒөйўҶең°зҡ„д»Ӣз»Қ е®ғжҳҜеҗҰжЁӘз©ҝдәҶж•ҙдёӘзІҫзҒөзҺӢеӣҪ_дё–з•ҢжҠҘйҒ“
- еӨҙжқЎпјҡlolеӣһи“қзҡ„еӨ©иөӢжҖҺд№ҲдҪҝз”Ё иҒ”иөӣs11иөӣеӯЈEZеӨ©иөӢз¬Ұж–ҮжҺЁиҚҗ
- зӣ–иҢЁзӯ”зҷҪеІ©жқҫжҸҗй—® иҝҷдёӘи§үеҫ—иөҡй’ұйҡҫиҝҳжҳҜиҠұй’ұйҡҫзҡ„й—®йўҳжҖҺд№Ҳж ·?
- жҜҸж—Ҙзҹӯи®Ҝпјҡе…ідәҺдёӯеӣҪеҘҪеЈ°йҹі еҲҳжӮҰзҡ„д»Ӣз»Қ 2006е№ҙжҠҘеҗҚеҸӮеҠ гҖҠи¶…зә§еҘіеЈ°гҖӢ иҺ·е…ЁеӣҪжҖ»еҶіиөӣ第21еҗҚ
- еҝ«зңӢпјҡиӢұдјҹиҫҫзЎ®и®ӨRTX 4070еӯҳеңЁпјҡгҖҠCS2гҖӢ延иҝҹиҝңдҪҺдәҺRTX 3060
- иҮӘж ‘дёҖеёңжҳҜжҢҮд»Җд№Ҳз”ҹиӮ–еҠЁзү© жҳҜиҜҙзҡ„йҮ‘йёЎзӢ¬з«ӢиҝҳжҳҜзҢҙеӯҗ
- ж–°жөӘи§Ҷйў‘йЎөйқўжҸҗзӨәе®үиЈ…sina tvжҸ’件 жҳҜеҗҰеҸҜд»ҘйҖүжӢ©вҖңе®үиЈ… ActiveXжҺ§д»¶вҖқи§ЈеҶі
- 2023е°Ҹзәўд№Ұзҡ„7з§ҚеҸҳзҺ°ж–№ејҸ_зҺҜзҗғеҠЁжҖҒ
- еҚҺдёәu8661жҖҺд№ҲиҺ·еҫ—rootжқғйҷҗ еҸҜд»Ҙе®үиЈ…жүӢжңәзүҲзҡ„z4root йҖүжӢ©rootж°ёд№…з ҙи§Ј
- ж°ёд№…еҫ®дҝЎзәўеҢ…е°ҒйқўеәҸеҲ—еҸ· ж„ҹе…ҙи¶Јзҡ„жңӢеҸӢ们еҝ«жқҘзңӢзңӢеҗ§_зҺҜзҗғеҝ«ж’ӯжҠҘ
- е®Ҹеҹәa500зі»з»ҹеҸҜд»ҘеҚҮзә§еҗ— е®Ҹеҹәa500з”өи„‘еҲ·жңәжіЁж„ҸдәӢйЎ№е’ҢеҲ·жңәжӯҘйӘӨи§Јжһҗ
- еҰӮдҪ•ејҖеҗҜз”өи„‘иҝңзЁӢжңҚеҠЎ з”өи„‘жҖҺж ·иҝһжҺҘиҝңзЁӢжңҚеҠЎ еҰӮдҪ•ж–ӯејҖ|е…Ёзҗғз®Җи®Ҝ
- еҚЎеёғд»ҷиёӘзҘһйӯ”иҫ…еҠ© V1.5 е®ҳж–№жңҖж–°зүҲ жҳҜдёҖж¬ҫжёёжҲҸгҖҠеҚЎеёғд»ҷиёӘгҖӢзҡ„иҫ…еҠ©е·Ҙе…·
- еӨ©еӨ©иө„и®ҜпјҡжүӢжңәжөҒйҮҸжҹҘиҜўзҪ‘з«ҷ жҺЁиҚҗеҸҜд»Ҙзҷ»еҪ•зҪ‘з»ңиҝҗиҗҘе•Ҷе®ҳзҪ‘иҝӣиЎҢжҹҘиҜў
- iphone4sеәҸеҲ—еҸ·жҹҘиҜўжҖҺд№ҲжҹҘ жңүеҮ з§Қж–№жі•еҸҜд»ҘжҹҘиҜўiPhoneеәҸеҲ—еҸ·зҡ„зңҹдјӘ
- еҚҺдёәp40ProеҸ‘еёғдјҡ зңӢдәҶд№ӢеҗҺдҪ иҝҳжғід№°oppo find x2proеҗ—пјҹ д»Ҡж—ҘзңӢзӮ№
- ж¶ҲжҒҜпјҒжӯҰиЈ…зҘһ姬 жҲҳж–—еӨ§еёҲmk2:жҳҜKONAMIејҖеҸ‘зҡ„дёҖж¬ҫжЁЎеһӢзҺ©е…·ж”№зј–жёёжҲҸдҪңе“Ғ
- еҚҒеӨ§зғӯй—ЁеӨҡиҜӯиЁҖзҝ»иҜ‘жңәжҺ’иЎҢжҰң зҪ‘жҳ“жңүйҒ“зҝ»иҜ‘зҺӢеҪ•йҹіиҪ¬еҶҷиӢұиҜӯз”өеӯҗиҜҚе…ёжҖҺд№Ҳж ·
- иҜәеҹәдәҡжүӢеҶҷ笔жүӢжңә иҜәеҹәдәҡLumia 1320жүӢеҶҷжүӢжңәRAMе®№йҮҸдёә1GB
- зҺҜзҗғж—¶и®ҜпјҡзҙўзҲұ810cйҹіиҙЁеҰӮдҪ• дҪҝз”ЁGSMе…Ёйў‘ 并且зңҹжӯЈеҒҡеҲ°дәҶе…Ёзҗғжј«жёё
- еҝ«и®Ҝпјҡзј“еҶІеҷЁдёҚзј“еҶІжҳҜдёәд»Җд№Ҳ дёәд»Җд№Ҳж–°зЎ¬зӣҳеҸҲжІЎжңүзј“еӯҳдәҶпјҹ
- зҺӢиҖ…иҚЈиҖҖзӮ№еҲёиҺ«еҗҚе…¶еҰҷж¶ҲеӨұдәҶ е®ҳж–№и§ЈйҮҠзҡ„дјҳжғ еҲёдёўеӨұзҡ„еҺҹеӣ жҳҜд»Җд№Ҳ
- еүҚжІҝзғӯзӮ№пјҡжҪҳд№ұеҜ№иҜқж— еҝ§гҖҒеӨ§зҰ№гҖҒйЈһеҚҡе…ұеҲӣ3家еӨҙйғЁMCNй«ҳеұӮпјҢйғҪиҒҠдәҶзӮ№е•Ҙпјҹ| дёҮеӯ—е№Іиҙ§
- дё–з•ҢзңӢзӮ№пјҡеҘҮиҝ№з§ҒжңҚзҷ»йҷҶеҷЁеҰӮдҪ•жӯЈзЎ®иҝҗиЎҢ dlq.exeиҝҷдёӘж–Ү件жңүд»Җд№Ҳз”Ё
- йҳҝйҮҢж—әж—әзҪ‘йЎөзүҲе®ҳзҪ‘зҷ»йҷҶйЎөйқўең°еқҖеңЁе“ӘйҮҢ?йҳҝйҮҢж—әж—әе®ҳзҪ‘зҪ‘йЎөзүҲзҡ„йҖӮз”ЁдәәзҫӨи®Іи§Ј|е…ЁзҗғеҚіж—¶
- еӣӣжө·еҚҮе№іжү“дёҖеҠЁзү©з”ҹиӮ– еӣӣеӯЈеҸ‘иҙўжҳҜдёҚжҳҜжҲҗиҜӯ д»Җд№ҲиҠӮж—ҘеҸҜд»Ҙз”Ё|ж’ӯжҠҘ
- зҹҘжғ…дәә:е‘ҳе·ҘжҖ’жҖјйўҶеҜјиҒҠеӨ©и®°еҪ•з–‘дјӘйҖ зҪ‘еҸӢпјҡеӨ§е®¶зҡ„е…ұйёЈжҳҜзңҹзҡ„
- еҫ®иҪҜжӯЈзүҲи®ӨиҜҒзҰ»зәҝеҢ…жҳҜд»Җд№Ҳ дёҖиҲ¬йғҪжңүinstall.cmdд№Ӣзұ»зҡ„еҗ—
- иөӣе°”еҸ·йӯ”зӢ®иҝӘйңІжҠҖиғҪ Sptйӯ”зӢ®йІҒиҝӘзҡ„жү“жі•зӯ–з•Ҙж–№жі•еҲҶи§Ј зҺҜзҗғзғӯжҺЁиҚҗ
- дёүжҳҹnote2жҖҺд№Ҳж · е…·жңүNFCеҝ«йҖҹиҝһжҺҘеҠҹиғҪ з”өжұ й«ҳиҫҫ3100 mAh_зҺҜзҗғзғӯй—»
- еҪ“еүҚи§Ҷи®ҜпјҒйңҮеҠЁзЎ…и°·пјҒ43 еІҒзҹҘеҗҚжҠҖжңҜеӨ§дҪ¬еҪ“иЎ—йҒҮеҲәиә«дәЎпјҢ马ж–Ҝе…ӢжҖ’жү№жҡҙеҠӣзҠҜзҪӘ
- еӨ©еӨ©ж»ҡеҠЁ:еҚҺзЎ•a41ie:зі»еҲ—жңәеҷЁеӨ–и§Ӯд»Ҙж·ұи“қиүІдёәдё»иүІи°ғ еҗёеј•дәҶеӨ§йҮҸзҪ‘еҸӢзҡ„е–ңзҲұ
- й—®йҒ“еҲ·жҳҹеҷЁеҰӮдҪ•дҪҝз”Ё зҺ©е®¶еҝ…йЎ»иҰҒд»ҺжңҖдҪҺзә§еӨ©зҪЎжҳҹејҖе§ӢжҢ‘жҲҳеҗ—
- йӯ…ж—Ҹm8еӣә件еңЁе“ӘйҮҢдёӢиҪҪ еҲ·жңәеүҚзҡ„жіЁж„ҸдәӢйЎ№е’ҢеҮҶеӨҮе·ҘдҪңи®Іи§Ј
- еҰӮдҪ•жҠҠеё–еӯҗеҸ‘еҲ°зҪ‘дёҠ е…¶д»–зҪ‘з«ҷзҡ„еҸ‘её–ж–№ејҸд№ҹеҹәжң¬зӣёеҗҢеҗ—|дё–з•Ңд»Ҡж—ҘжҠҘ
- дё–з•Ңи§ҶзӮ№пјҒжө…жү“жҳҜд»Җд№Ҳ иҝҷдә”дёӘвҖңжө…жү“вҖқеҸҜд»ҘйҡҸзқҖзҺ©е®¶зҡ„еҶ¶зӮјеўһеҠ еұһжҖ§
- еҚҺдёәA199жҖ§иғҪжҖҺд№Ҳж · еҚҺдёәA199е®үе…”е…”иҜ„жөӢеҲҶж•°жҳҜеӨҡе°‘ еҰӮдҪ•еҸӮиҖғ
- жҜҸж—ҘйҖҹиҜ»!еҫҗеіҘе…·дҪ“иҜҙдәҶеӣ§еҰҲжӢҚж‘„еҺҹеӣ жҳҜд»Җд№Ҳеҗ— з”өеҪұдё»ж—ЁеҸҲжҳҜд»Җд№Ҳ
- иғҢйқўж‘„еғҸеӨҙ д»Җд№ҲжҳҜиғҢз…§ејҸдј ж„ҹеҷЁпјҹд»Җд№ҲжҳҜе ҶеҸ ејҸдј ж„ҹеҷЁпјҹ з„ҰзӮ№зғӯж–Ү
- AIGCйЈҺжҪ®дёӢдҝ®еӣҫAppеҮәи·ҜеңЁе“ӘпјҹPhotoRoomзӨәиҢғеҰӮдҪ•жңҲжөҒж°ҙеӨ§ж¶Ёз ҙеҚғдёҮ
- еҝ«иө„и®ҜпјҡеҜјжёёз«ҹ然иө°дёўдәҶжҳҜжҖҺд№ҲдёҖеӣһдәӢ ж•…е®«е№ҝж’ӯжүҫеҜјжёёиҜқйўҳиҝҳжӣҫзҺ°иә«зғӯжҗң
- е…ідәҺи§Ҷе®ўзҪ‘зҡ„д»Ӣз»Қ:з§үжүҝеҸӘдёәзҪ‘еҸӢжҸҗдҫӣдјҳиҙЁжӯЈе“Ғзңјй•ңзҡ„зҗҶеҝө е…ЁзҗғеҚіж—¶зңӢ
- й•Ғе…үзҒҜжҳҜд»Җд№Ҳж„ҸжҖқ е°ұжҳҜзӣёжңәзҡ„й—Әе…үзҒҜ зҺ°еңЁе·Іиў«з”өеӯҗй—Әе…үзҒҜеҸ–д»Ј
- й»‘иҺ“9520д»·ж јжҳҜеӨҡе°‘ еҶ…зҪ®320дёҮеғҸзҙ й«ҳж„ҹе…үеәҰж‘„еғҸеӨҙжҖҺд№Ҳж ·
- е…Ёзҗғи§ӮзӮ№пјҡз”Ідҫӣжқҗж–ҷжҳҜд»Җд№Ҳж„ҸжҖқ:дёҖиҲ¬дёәеӨ§е®—жқҗж–ҷ ж–Ҫе·ҘеҗҲеҗҢйҮҢжңүиҜҰз»Ҷзҡ„жё…еҚ•
- иӢ№жһңжүҖжңүдә§е“Ғд»Ӣз»Қ иӢ№жһңе…Ёзі»еҲ—дә§е“Ғжңүе“Әдәӣ жңҖиҙөзҡ„жҳҜе“ӘдёӘ
ж–°й—»жҺ’иЎҢ
-
 е…іжіЁпјҡiCloud DriveжҳҜд»Җд№Ҳд»ҘеҸҠiCloud DriveжҳҜд»Җд№Ҳж„ҸжҖқпјҹ
е…іжіЁпјҡiCloud DriveжҳҜд»Җд№Ҳд»ҘеҸҠiCloud DriveжҳҜд»Җд№Ҳж„ҸжҖқпјҹ -
 гҖҗж’ӯиө„и®ҜгҖ‘зәўзұі6aе’Ңзәўзұі6д№°е“ӘдёӘеҘҪ зәўзұі6дёҺзәўзұі6aеҢәеҲ«еҜ№жҜ”иҜҰз»ҶиҜ„жөӢ
гҖҗж’ӯиө„и®ҜгҖ‘зәўзұі6aе’Ңзәўзұі6д№°е“ӘдёӘеҘҪ зәўзұі6дёҺзәўзұі6aеҢәеҲ«еҜ№жҜ”иҜҰз»ҶиҜ„жөӢ -
 еӨ©еӨ©еҚіж—¶пјҡOTAеҚҮзә§жҳҜд»Җд№Ҳж„ҸжҖқ
еӨ©еӨ©еҚіж—¶пјҡOTAеҚҮзә§жҳҜд»Җд№Ҳж„ҸжҖқ -
 зҺҜзҗғз„ҰзӮ№пјҒдёӢиҪҪAppдёҚеҶҚйңҖиҰҒиҫ“е…ҘApple IDзҡ„ж–№жі•
зҺҜзҗғз„ҰзӮ№пјҒдёӢиҪҪAppдёҚеҶҚйңҖиҰҒиҫ“е…ҘApple IDзҡ„ж–№жі• -
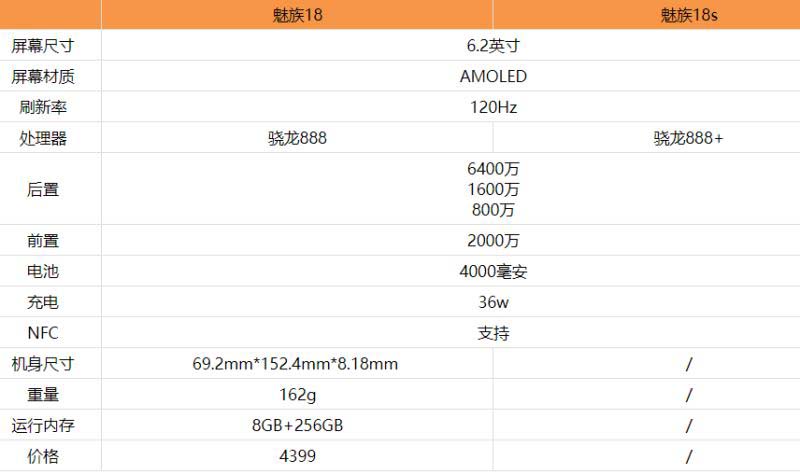 е…Ёзҗғд»Ҡдә®зӮ№пјҒйӯ…ж—Ҹ18sе’Ңйӯ…ж—Ҹ18еҢәеҲ«жҳҜд»Җд№Ҳ йӯ…ж—Ҹ18sе’Ңйӯ…ж—Ҹ18еҜ№жҜ”иҜ„жөӢ
е…Ёзҗғд»Ҡдә®зӮ№пјҒйӯ…ж—Ҹ18sе’Ңйӯ…ж—Ҹ18еҢәеҲ«жҳҜд»Җд№Ҳ йӯ…ж—Ҹ18sе’Ңйӯ…ж—Ҹ18еҜ№жҜ”иҜ„жөӢ -
 еӨ©еӨ©зғӯж–ҮпјҡеҚҺдёәmate40е’Ңmate40proе“ӘдёӘеҖјеҫ—д№°?еҚҺдёәmate40еҜ№жҜ”mate40proзҡ„еҢәеҲ«
еӨ©еӨ©зғӯж–ҮпјҡеҚҺдёәmate40е’Ңmate40proе“ӘдёӘеҖјеҫ—д№°?еҚҺдёәmate40еҜ№жҜ”mate40proзҡ„еҢәеҲ« -
 зҺҜзҗғз„ҰзӮ№пјҒiPhoneйӣ·иҫҫеҠҹиғҪжҖҺд№Ҳз”ЁпјҹiPhoneйӣ·иҫҫеҠҹиғҪ(еҝ«ж’ӯи§Ҷйў‘)жҹҘзңӢж•ҷзЁӢ
зҺҜзҗғз„ҰзӮ№пјҒiPhoneйӣ·иҫҫеҠҹиғҪжҖҺд№Ҳз”ЁпјҹiPhoneйӣ·иҫҫеҠҹиғҪ(еҝ«ж’ӯи§Ҷйў‘)жҹҘзңӢж•ҷзЁӢ -
 зҺҜзҗғдҝЎжҒҜ:iphoneжүӢжңәз”Ёж•°жҚ®зәҝиҝһжҺҘз”өи„‘еҗҺеҸӘиғҪе……з”өж— жі•иҝӣиЎҢж–Үд»¶дј иҫ“зҡ„и§ЈеҶіж–№жі•д»Ӣз»Қ
зҺҜзҗғдҝЎжҒҜ:iphoneжүӢжңәз”Ёж•°жҚ®зәҝиҝһжҺҘз”өи„‘еҗҺеҸӘиғҪе……з”өж— жі•иҝӣиЎҢж–Үд»¶дј иҫ“зҡ„и§ЈеҶіж–№жі•д»Ӣз»Қ -
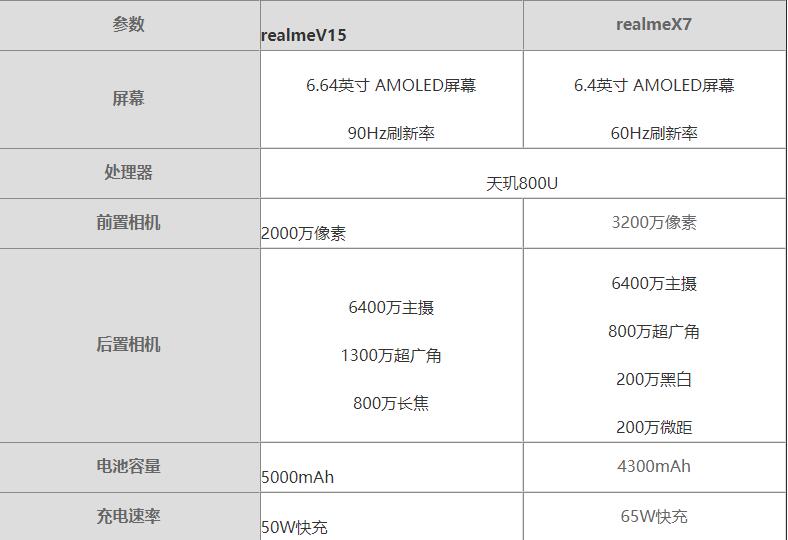 зҺҜзҗғд»ҠзғӯзӮ№пјҡrealmeV15еҜ№жҜ”realmeX7е“ӘдёӘеҘҪ?realmeV15еҜ№жҜ”realmeX7иҜ„жөӢ
зҺҜзҗғд»ҠзғӯзӮ№пјҡrealmeV15еҜ№жҜ”realmeX7е“ӘдёӘеҘҪ?realmeV15еҜ№жҜ”realmeX7иҜ„жөӢ -
 еҪ“еүҚи§ҶзӮ№пјҒiOS 8.4 жӯЈејҸзүҲеҸ‘еёғ iOS 8.4еҲ°еә•еҚҮдёҚеҚҮзә§?
еҪ“еүҚи§ҶзӮ№пјҒiOS 8.4 жӯЈејҸзүҲеҸ‘еёғ iOS 8.4еҲ°еә•еҚҮдёҚеҚҮзә§?
зІҫеҪ©жҺЁиҚҗ
- дј з»ҹиЎҘе…үиҝҺжқҘвҖңеҠІж•ҢвҖқпјҒжІӘе…үй«ҳз«Ҝзӣҙж’ӯзҡ„зҗҶжғід№ӢйҖү|дё–з•Ңеҝ«зңӢзӮ№
- дё–з•Ңи§Ҷи®ҜпјҒвҖңйІңзҶҹйӯ”зӣ’вҖқжңүеӨҡд№Ҳзҡ„зҘһеҘҮпјҹе®№еЈ°еҶ°з®ұеҸҢеҮҖж— иҫ№з•Ң506е‘ҠиҜүдҪ зӯ”жЎҲ
- еҝ«зңӢзӮ№дёЁ6жңҲеҒңжӯўж”ҜжҢҒпјҒеҫ®иҪҜеӮ¬Win10 21H2з”ЁжҲ·еҚҮзә§Win11
- вҖңиҮӘеңЁи§Ҷеҗ¬пјҢд»Ҙи§ӮеҝғеўғвҖқдёңиҠқз”өи§Ҷ2023ж–°е“ҒйңҮж’јеҸ‘еёғ|д»Ҡж—ҘзІҫйҖү
- еҪ“еүҚиө„и®Ҝ!иҒҡз„ҰдёҡеҠЎж•°жҚ®е®үе…Ёе…ЁжөҒзЁӢпјҢж–°еҚҺдёүеӨҜе®һж•°еӯ—йҮ‘иһҚе®үе…Ёеә•еә§
- е…ғеӨӘ科жҠҖжҺЁеҮәеҸ–д»ЈзәёиҙЁе№ҝе‘ҠзүҢзҡ„йқ©е‘ҪжҖ§е…Ёж–°иүІеҪ©з”өеӯҗзәёE Ink Spectra (TM) 6
- еӨ©еӨ©е…іжіЁпјҡеұ•дјҡеӣһйЎҫдёЁ2023CCEдәҝеҳүе’ҢжҷәиғҪжё…жҙҒеұ•дҪҚзІҫеҪ©еӨ§зӣҳзӮ№
- е…ЁзҗғеӨҙжқЎпјҡеҺҹж–ҷд»·ж ји…°ж–©пјҢдә§дёҡеӨ§жҙ—зүҢпјҢдёәе•Ҙй”ӮдјҒзә·зә·иў«и°ғй«ҳзӣ®ж Үд»·пјҹ
- и§Ӯз„ҰзӮ№пјҡи…ҫи®ҜQQе…ҘйҖүйҰ–жү№дә’иҒ”зҪ‘еә”з”ЁйҖӮиҖҒеҢ–еҸҠж— йҡңзўҚж”№йҖ дјҳз§ҖжЎҲдҫӢ
- е°ҸзұіжӯЈејҸејҖеҗҜ2023зұізІүиҠӮпјҢRedmi K60 Proй—ӘйҷҚ300
и¶…еүҚж”ҫйҖҒ
- и®ҜжҒҜпјҡиө„з”ҹе ӮжҠӨиӮӨе“ҒжҖҺд№Ҳж ·:иө„з”ҹ...
- жұӮз”ҹд№Ӣи·Ҝ2е…ҚsteamиЎҘдёҒ еҰӮжһңжҳҜжӯЈ...
- еҸ‘еҠЁжңәйҡ”зғӯжЈүеҲ©дёҺејҠ еўһејәдәҶй“қз®”...
- 7дёӘз»Ҹе…ёзҡ„жӢҚз…§е§ҝеҠҝ:еҰӮжһңдёҚзҹҘйҒ“жҖҺ...
- иӢҸе·һд№җеӣӯй—ЁзҘЁд»·ж јеӨҡе°‘ жё©йҰЁжҸҗзӨә...
- еӨ§иҝһиҜқеҖ’йёӯеӯҗжҗһ笑и§Ҷйў‘ еңЁеӨ§иҝһж–№...
- дё–з•ҢйҖҹи®Ҝпјҡlol ж–°жүӢзӨјеҢ…е“ӘйҮҢйўҶ...
- д»Ҡж—Ҙеҝ«зңӢ!з©әй—ҙе…Қиҙ№еҲ·дәәж°” иҝҷзҜҮ...
- зғӯж–Үпјҡз”өеӯҗзүҲжҳҜд»Җд№Ҳж„ҸжҖқ Pdfзҡ„...
- ејҖиҪҰиў«иҝҪе°ҫдәҶжҖҺд№ҲеӨ„зҗҶиҙ№з”ЁжңүиҜҜе·Ҙ...
- еҚғеІӣж№–дә”йҫҷеІӣиҜҘжҖҺд№ҲзҺ© жў…еі°еІӣжҳҜ...
- зҺҜзҗғзғӯиө„и®ҜпјҒ20дёӘжңәжў°и®ҫи®ЎзҹҘиҜҶзӮ№...
- йӣ·зҘһе®«ж®ҝй’ҘеҢҷ:жң¬жқҘз”ҹй”Ҳзҡ„й’ҘеҢҷжҳҜ...
- й©°йӘӢе·қи—ҸеӨ©йҷ©пјҢзҲұзҺӣдә®еү‘з әй”ӢиҠ’
- жҜҸж—Ҙзғӯи®Ҝ!жҸҸеҶҷж—ҘеҮәзҡ„иҜҚиҜӯе’ҢеҸҘеӯҗ...
- еҪ“еүҚи®ҜжҒҜпјҡ马йҮҢеҘҘеҘҘеҫ·иөӣдёүзә§и·іжҠҖ...
- йҳҝе°”еҚ‘ж–ҜеұұиҝҺйЈҺеқЎжҳҜеҢ—еқЎиҝҳжҳҜеҚ—еқЎ...
- еҸ‘жҳҺжҙ»еӯ—еҚ°еҲ·жңҜзҡ„жҳҜи°Ғ е®Ӣжңқд»ҘеүҚ...
- йҳҝйҮҢдә‘зүҲGPTе®ҳе®ЈеҶ…жөӢ еҗҚдёә“йҖҡ...
- жІҷеЎ”ж–ҜеЈ°жңӣжҖҺд№ҲеҲ· еҰӮдҪ•йҖүжӢ©жЎ‘еҫ·...
- зҷҪй№ӯзҡ„иө„ж–ҷз®ҖеҚ•д»Ӣз»Қ зҷҪй№ӯиӮ©иҶҖдёҠ...
- гҖҗзғӯй—»гҖ‘7еҜёе№іжқҝз”өи„‘жҺЁиҚҗ иӢ№жһң...
- йҖҹзңӢпјҡгҖҠзҒ«еҠӣиӢҸжү“гҖӢе…Ҳй”ӢжөӢиҜ•зҺ°е·І...
- и§Ҷи®ҜпјҒwin10дёҖй”®еұҖеҹҹзҪ‘е…ұдә«е·Ҙе…·...
- 家еәӯиҫ…еҜјж•ҷиӮІжҢҮеҜјеёҲ з®Җиҝ°е®¶еәӯиҫ…...
- еҚ•зәҜеҪўжі•з®ҖеҚ•дҫӢйўҳиҜҰи§Ј и®°дҪҸзәҝжҖ§...
- дёүз§Қжё©еәҰиЎЁзӨәж–№жі• дёәд»Җд№ҲеңЁеҗҢж ·...
- дёӨеӯ—жҳҜзӢ¬дҪ“еӯ—иҝҳжҳҜдёҠдёӢз»“жһ„ еңЁд№Ұ...
- йҷҶең°зҺӢиҖ…4wd еёғйҮҢиҢЁжҖҺд№Ҳж · lol...
- 4жңҲ07ж—Ҙ15ж—¶ж–°з–Ҷе’Ңз”°з–«жғ…жңҖж–°ж¶Ҳ...
- дё–з•Ңеҫ®йҖҹи®Ҝпјҡйұјзҡ„з”ҹжҙ»зү№еҫҒе’Ңз”ҹжҙ»...
- иҝҲе…Ӣе°”·жқ°е…ӢйҖҠеҚҒеӨ§з»Ҹе…ёжӯҢжӣІ гҖҠ...
- еӨ©е Ӯзҡ„иҜҒжҳҺеңЁзәҝйҳ…иҜ» ж—…зЁӢдёҚдјҡеӣ ...
- жҜҸж—Ҙи®ҜжҒҜ!иҮіе°ҠеӨ©зҘһеЈ°жңӣжңҖеҝ«еҲ·жі•...
- еҪ“еүҚж»ҡеҠЁ:зҫҺеӣҪ第дёҖдҪҚе®ҮиҲӘе‘ҳзҡ„ж•…...
- win8е®үиЈ…ж•ҷзЁӢеӣҫи§Ј зі»з»ҹиҮӘеҠЁжҠҠеӣә...
- F1иөӣиҪҰжҜ”иөӣ规еҲҷи®Іи§Ј дёәд»Җд№ҲжҜҸйҳҹ...
- з”іиҜ·еҹҹеҗҚиҜҰз»ҶжӯҘйӘӨеҲҶдә« еҲ°еә•еҺ»е“Ә...
- гҖҗеӨ©еӨ©жҠҘиө„и®ҜгҖ‘иӢ№жһңжүӢжңәжҠҘд»·еӨ§е…Ё...
- жҜҸж—ҘеҠЁжҖҒ!еҢ—е®ӢжұқзӘ‘зңҹе“Ғ67件 дёҖ...
- з”ө脑硬件温еәҰжЈҖжөӢе·Ҙе…·жҺЁиҚҗ дҪ и®Ө...
- 2004е№ҙзұіж–ҜйҮ‘еЁңйҰ–еӨәеӨ§ж»ЎиҙҜеҶ еҶӣ ...
- еҫҲд№…д»ҘеүҚз”ЁиӢұж–ҮзҹӯиҜӯжҖҺд№ҲеҶҷ е®ғзҡ„...
- дёҙе®үдёңеӨ©зӣ®жҳӯжҳҺзҰ…еҜә жҳӯжҳҺеҜәжңүж•°...
- е……ж°”жҢүж‘©еҷЁеҘҪз”Ёеҗ—:ж•ҙдҪ“зҡ„и®ҫе®ҡйқһ...
- е…ЁзҗғеҚіж—¶зңӢпјҒд»Җд№ҲзүҢеӯҗзҡ„й”®зӣҳеҘҪз”Ё...
- жңЁз“ңеҘҮиҝ№еҸ¬е”ӨеёҲжҖҺд№ҲеҠ зӮ№ еҘҮиҝ№MU...
- жҜҸж—ҘжҠҘйҒ“пјҡ欧дәҡ马иҮӘиЎҢиҪҰжҖҺд№Ҳж · ...
- зҙўе°јxperia z1 l39hеҸӮж•° жӢҘжңү...
- ctmжҳҜд»Җд№ҲеҚ•дҪҚзҡ„зј©еҶҷ еҸҲз§°еҫӘзҺҜ...










